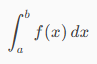
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

10-07-2025 - Mathematical Analysis - Integration Methods [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-61)
Integration Methods

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
First of all we need to clarify the concept of integral. Very often explained in a way that is too technical to always be difficult to understand.
I try to explain it as I would have liked it to have been explained to me.
The integral in mathematics is a fundamental concept and represents the area under the curve of a function in a certain interval. The definite integral therefore provides a numerical value that represents the area.
The graph below shows the integral of the function
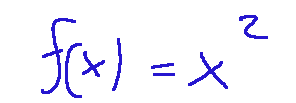
graph below
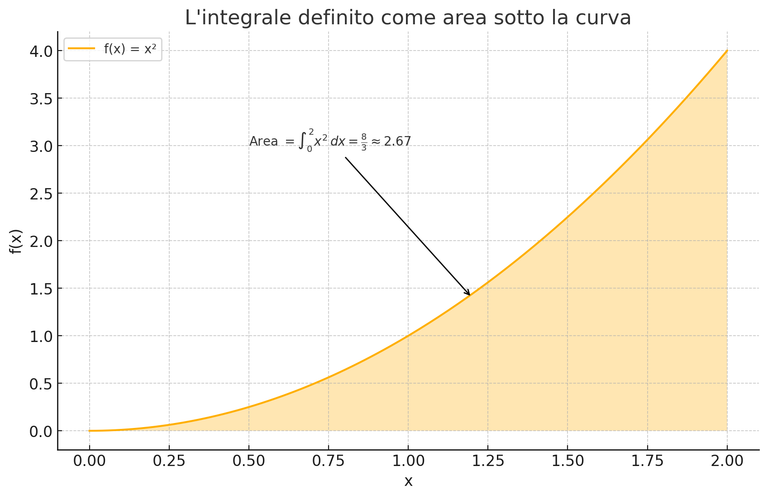
image created with artificial intelligence, the software used is ChatGPT
The integral represents the area, i.e. the orange zone. So the integral gives us an area.
let's proceed with a clarification
When we talk about integral, since we have clarified that it is an area, we must also define the limits of the area of which we want to know the area.
Let's always take the graph above as an example.
If we take a look at the function we see that the orange area of the graph goes from zero to 2. So an integral is defined not only by the function, but also by a starting value of x and a finishing value of x.
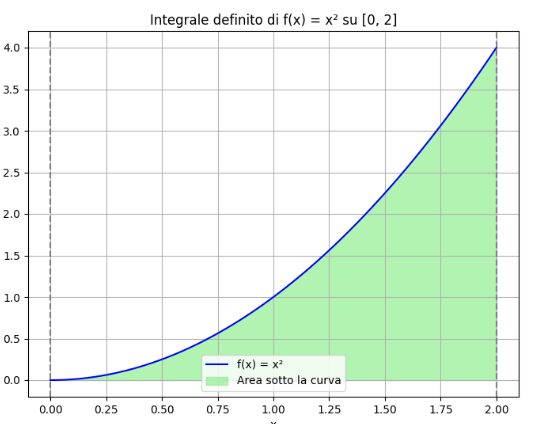
So in the graph it actually represents the following:
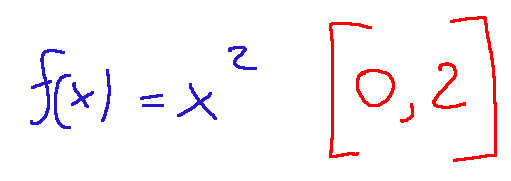
That is, the area under the curve defined by the function f(x) = x^2 in the interval [0,2]
Below is how the integral we just talked about is mathematically described.
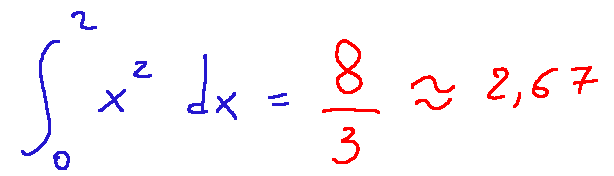
how do you read it?
What we just wrote is read as follows.
Integral from 0 to 2 of x squared on dx is equal to 8/3.
The part where dx is written means more precisely that the integral, i.e. the area we want to calculate is on the x-axis. dx specifies how much we are adding (what is the basic infinitesimal) and on which axis this operation is done
Technical definition of integral
An integral is used to add up many infinitesimal contributions of a quantity.
Integration methods
Talking about integration methods means describing the set of algebraic, analytical or numerical techniques that allow you to calculate an integral.
There are different integration methods, the main ones are as follows:
-Integration by parts
-Integration by substitution
-Integration by decomposition into simple fractions
-Integration by trigonometric substitution
Example of an exercise
Let's try to calculate the following integral.
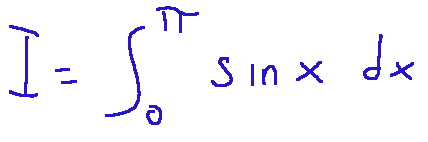
First, we notice that the interval goes from 0 to π
-step 01-
First we should find a primitive which is the following
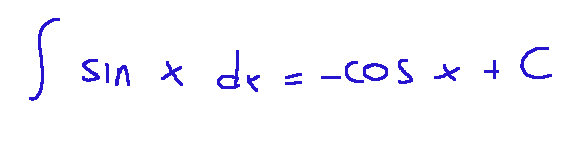
-step 02-
Now let's apply the following calculation
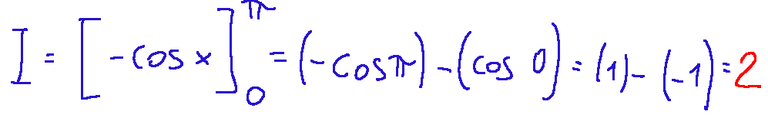
This integral represents the signed area under the curve y = sin x, in the interval that goes from x=0 to x=π. Since sin x in that particular interval is positive, the area is 2 square units as can be seen from the formula reported above.
the graph
Here is how this integral is represented graphically
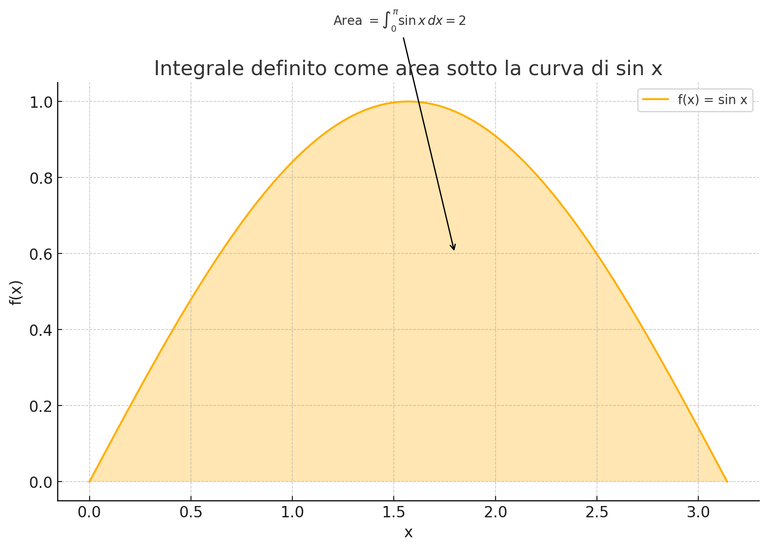
The orange region corresponds to the area under the curve of the function, that is, it corresponds to the integral.
Conclusions
I don't know if I succeeded in explaining in a simple way what an integral is, but the conclusion is the following, the integral of a function is a certain area of a certain function within a well-defined interval. However, with the graphs inserted in the post, in my opinion the concept is more understandable.
Question
Integrals were studied by both Newton and Leibniz, but did you know that the particular symbol that identifies it, that elongated "s" was thought up by the German mathematician Leibniz? Did you know that the elongated "s" was chosen because it was the abbreviation of the Latin word summa?

ITALIAN

10-07-2025 - Analisi Matematica - Metodi di integrazione [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-61)
Metodi di integrazione

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Prima di tutto dobbiamo chiarire il concetto di integrale. Molto spesso spiegato in maniera troppo tecnica da risultare sempre poco comprensibile.
Io provo a spiegarlo come avrei voluto che fosse stato spiegato a me.
L'integrale in matematica è un concetto fondamentale e rappresenta l'area sotto la curva di una funzione in un certo intervallo. L'integrale definito quindi fornisce un valore numerico che rappresenta l'area.
Nel grafico qui sotto è mostrato l'integrale della funzione
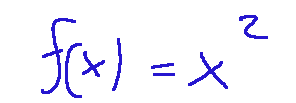
grafico qui sotto

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
L'integrale rappresenta l'area, cioè la zona arancione. Quindi l'integrale ci fornisce un'area.
procediamo con una precisazione
Quando parliamo di integrale, siccome abbiamo chiarito che è un area, dobbiamo definire anche i limiti della zona di cui vogliamo sapere l'area.
Prendiamo sempre come esempio il grafico riportato sopra.
Se diamo un'occhiata alla funzione vediamo che la zona arancione del grafico va da zero a 2. Quindi un integrale è definito non solo dalla funzione, ma anche da un valore di x di partenza ed un valore di x di arrivo.
Quindi in grafico rappresenta in realtà quanto segue:

Cioè l'area sotto alla curva definita dalla funzione f(x) = x^2 nell'intervallo [0,2]
Qui di seguito come di descrive matematicamente l'integrale di cui abbiamo appena parlato.
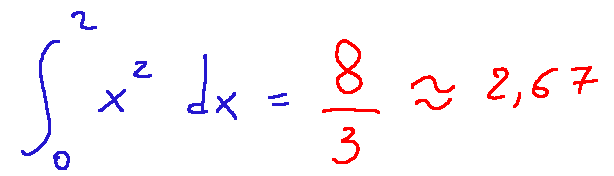
come si legge?
Quello che abbiamo appena scritto si legge come segue.
Integrale da 0 a 2 di x al quadrato in dx è uguale a 8/3.
La parte in cui è scritto dx significa più precisamente che l'integrale, cioè l'area che vogliamo calcolare è sull'asse x. dx specifica quanto stiamo sommando (qual è l'infinitesimo di base) e su quale asse viene fatta questa operazione
Definizione tecnica di integrale
Un integrale serve per fare la sommatoria di molti contributi infinitesimali di una grandezza.
Metodi di integrazione
Parlare di metodi di integrazione significa descrivere l'insieme di tecniche algebriche, analitiche o numeriche, che permettono di calcolare un integrale.
I metodo di integrazione sono diversi, qui di seguito i principali:
-Integrazioni per parti
-Integrazione per sostituzione
-Integrazione per decomposizione in fratti semplici
-Integrazione per sostituzione trigonometrica
Esempio di un esercizio
Proviamo a calcolare il seguente integrale.
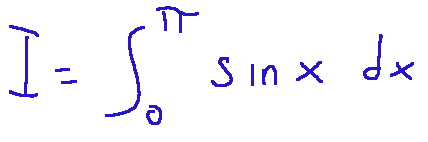
Intanto notiamo che l'intervallo va da 0 a π
-passo 01-
Per prima cosa dovremmo trovare una primitiva che è la seguente
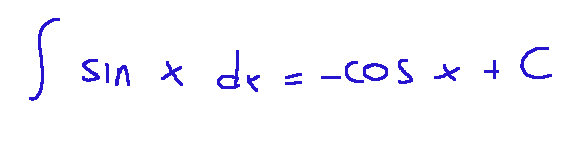
-passo 02-
Ora applichiamo il seguente calcolo
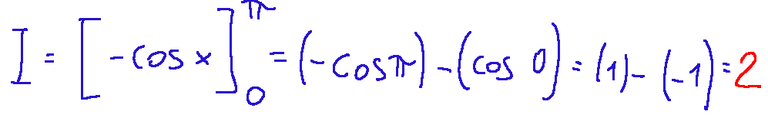
Questo integrale rappresenta l'area con segno sotto la curva y = sin x, nell'intervallo che va da x=0 a x=π. Siccome sin x in quel determinato intervallo è positiva, l'area è 2 unità quadrate come si nota dalla formula riportata qui sopra.
il grafico
Ecco come è rappresentato graficamente questo integrale

La regione arancione corrisponde all'area sotto la curva della funzione, cioè corrisponde all'integrale.
Conclusioni
Non so se sono riuscito nell'intento di spiegare in maniera semplice che cosa è un integrale, ma la conclusione è la seguente, l'integrale di una funzione è una determinata area di una determinata funzione all'interno di un intervallo ben definito. Comunque con i grafici inseriti nel post secondo me il concetto è più comprensibile.
Domanda
Gli integrali furono studiati sia da Newton che Leibniz, ma lo sapevate che il particolare simbolo che lo identifica, cioè quella "s" allungata fu pensata dal matematico tedesco Leibniz? Lo sapevate che venne scelta la “s” allungata perchè era l'abbreviazione della parola latina summa?
THE END