A me lo hanno spiegato (ed io continuo a spiegarlo in questo modo quando do ripezioni) proprio con l'area. Io parto da funzioni discrete, cioè da sommatorie di delta x grandi (che sono il sigma greco e il delta greco) e faccio vedere l'area dei singoli rettangoli di una funzione discreta istagrammica. Dopo faccio vedere come i delta x diventano sempre più piccoli fino a trasformarsi in dx infinitesimali e quindi a non avere più un istogramma ma una funzione continua. A quel punto la sommatoria diventa la somma di quei piccoli dx della funzione e non si scrive più come sigma greco ma col simbolo dell'integrale che alla fine è una S stilizzata.
Non so se ti ho reso l'idea.
!LOLZ
Hai reso benissimo l'idea!!! Direi che la tua spiegazione è ottima!!! Se ho capito bene parti da una spiegazione visiva per poi arrivare alla spiegazione completa dell'integrale. Quindi disegni gli istogrammi sotto la curva spiegando che più ce ne sono e più è preciso il calcolo dell'area. Se ho capito fai una cosa simile a quella che riporto qui sotto con la funzione f(x)=x^2 sull'intervallo [0,1]
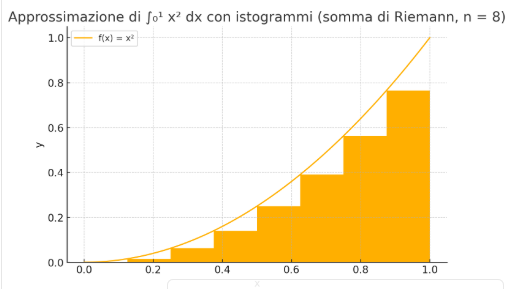
Grafico generato con Copilot
Esatto! x quadro è l'altezza del rettangolo in x1 e x2 e delta x è la base (x1 - x2) nel tuo esempio vale 0,2. Se tu fai la sommatoria delle aree del rettangolo approssimi l'area della funzione f(x) = x quadro. Approssimi perché mancano tutti le aree bianche tra la curva reale e i rettangoli. Se delta x diventa più piccino, i rettangoli diventano sempre più stretti e di più e gli spazi bianchi diventano meno, quindi la sommatoria delle aree dei rettangoli approssima sempre meglio l'area della curva. Finché x2 non tende a x1 e quindi il delta x tende a zero e diventa un infinitesimale dx che rappresenta un rettangolo con una base così piccola da essere una linea e così la somma di quelle linee non è più un'approssimazione ma l'area vera della curva. E come la calcoli l'area di una linea? Non puoi, quindi la sommatoria di una funzione discreta diventa un integrale.
!LOLZ
Grazie per aver lasciato questo commento.. praticamente se integrassi (nel senso di inserire), questo tuo commento alla mia spiegazione, forse otterrei la spiegazione perfetta dell'integrale!!! Uno dei miei obiettivi, per cui faccio questi post educativi, è anche quello di cercare spiegazioni facili per far comprendere certi concetti a più persone. Sono molto lontano dal raggiungere questo obiettivo, ma come vedi, ci sto provando. !PIZZA
but you didn't like it.
Credit: reddit
@stefano.massari, I sent you an $LOLZ on behalf of sissim72
(2/6)

PLAY & EARN $DOOM
At dive bars.
Credit: reddit
@stefano.massari, I sent you an $LOLZ on behalf of sissim72
(1/6)
NEW: Join LOLZ's Daily Earn and Burn Contest and win $LOLZ
