~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
12-02-2024 - Physics - Conduction in non-stationary regime [EN]-[IT]
Conduction in non-stationary regime
Let's take the case of a flat plate where a fluid flows along the sides and assume that there is no energy production.
In this case the thermal parameters will be independent of the temperature and the latter will be variable over time.
Below is the system taken as a case study.
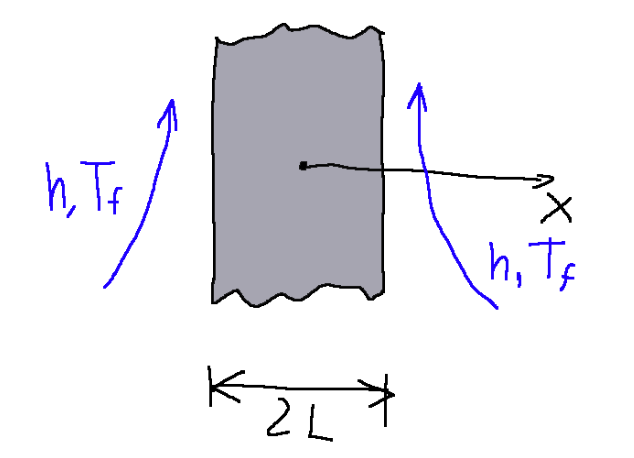
The formula that identifies the energy balance will be written as follows:
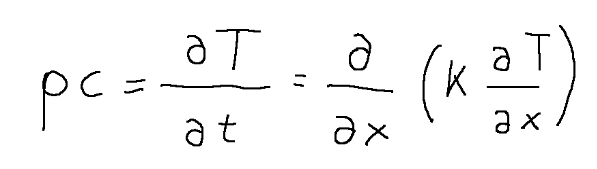
We must now add the initial condition T(t=0, x) = Ti = const and the boundary conditions which in this case are of the convective type. We will therefore have the system of these two equations:
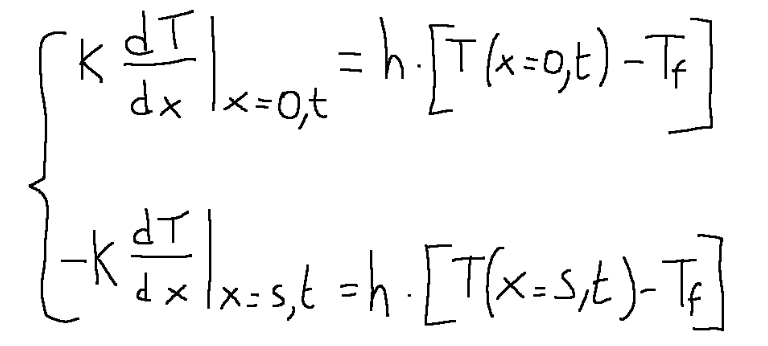
If we take the fluid that cools the plate as an example we will have the following temperature graph.
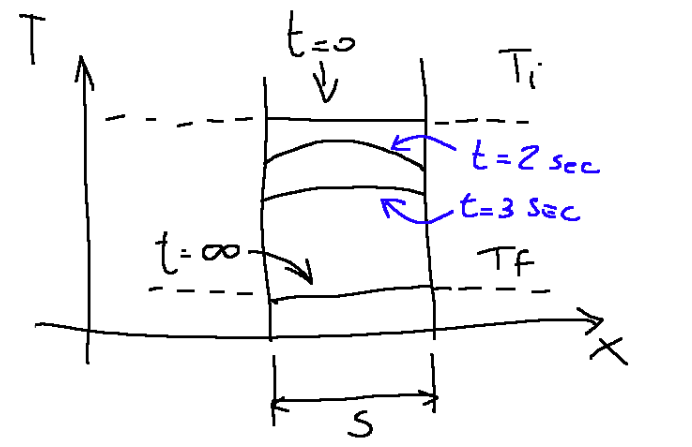
At this point we can deduce that the temperature will be a function of numerous variables.
For this reason it is advisable to make a dimensionality to simplify the problem.
So the first formula we saw at the beginning (I report it below)...
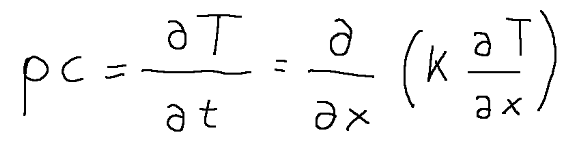
… can be rewritten in a dimensionless manner in the following way
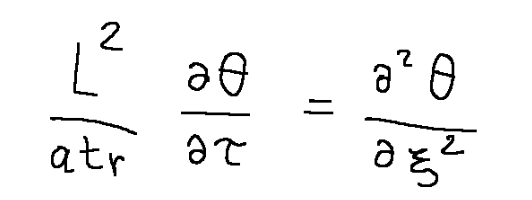
Now let's see how both the initial condition and the boundary conditions become.
Simplified initial condition
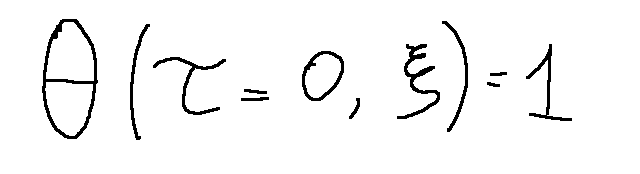
Simplified boundary conditions
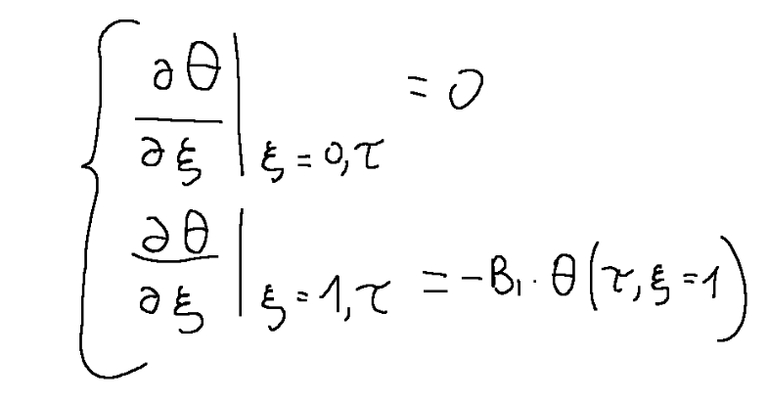
We note in these last equations the term Bi
This is called the Biot number which is the ratio of the conductive resistivity (inside the plate) over the convective resistivity (outside the plate).
The Biot number is a dimensionless group used mainly in fluid dynamics.
The name derives from the French physicist Jean-Baptiste Biot who lived between the end of the 1700s and the first half of the 1800s.
If Bi takes on very small values we notice that the temperature does not depend on the particular observation point inside the plate, but depends only on time.
Finally we will have that the solution will be the following:
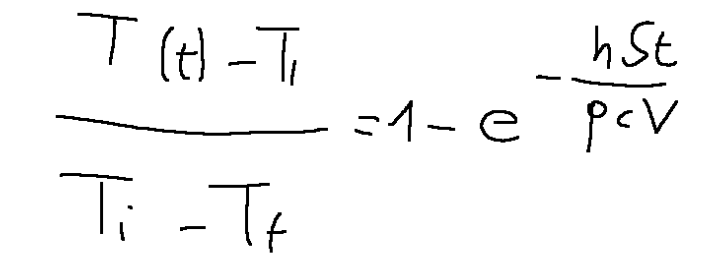
and the diagram will look like this.

Conclusions
The Biot number is the ratio of the conductive resistivity inside a plate to the convective resistivity outside that same plate.
Request
Have you ever studied conductive resistivity or convective resistivity?

12-02-2024 - Fisica - Conduzione in regime non stazionario [EN]-[IT]
Conduzione in regime non stazionario
Prendiamo il caso di una lastra piana dove ai lati scorre un fluido ed ipotizziamo che non ci sia produzione di energia.
In questo caso i parametri termici saranno indipendenti dalla temperatura e questa risulterà variabile nel tempo.
Qui di seguito il sistema preso come caso di studio.

La formula che identifica il bilancio dell’energia sarà scritta come segue:
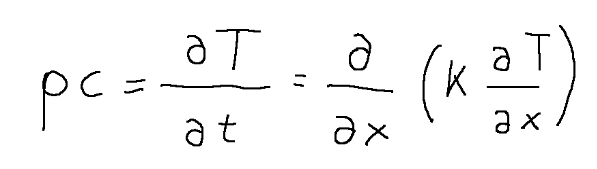
Dobbiamo ora aggiungere la condizione iniziale T(t=0, x) = Ti = cost e le condizioni al contorno che in questo caso sono di tipo convettivo. Avremo quindi il sistema di queste due equazioni:
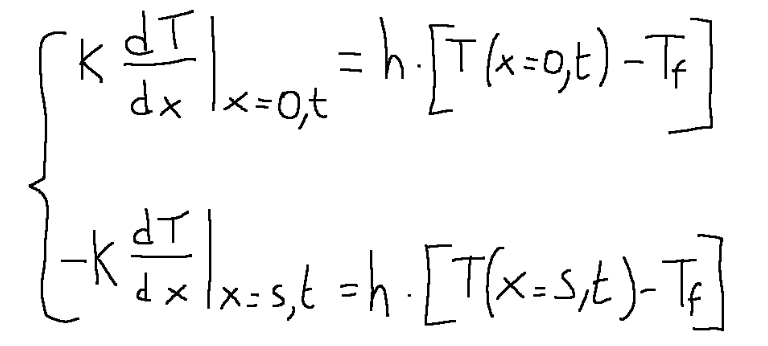
Se prendiamo come esempio il fluido che raffredda la piastra avremo il seguente grafico delle temperature.

A questo punto possiamo dedurre che la temperatura sarà in funzione di numerose variabili.
Per questo motivo conviene apportare una adimensionalizzazione per semplificare il problema.
Quindi la prima formula che abbiamo visto all’inizio (la riporto qui sotto)...
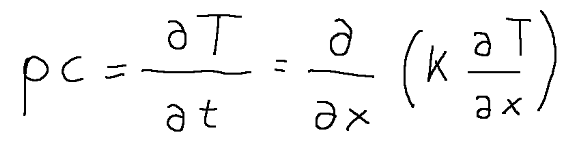
… può essere riscritta in maniera adimensionalizzata nella seguente maniera
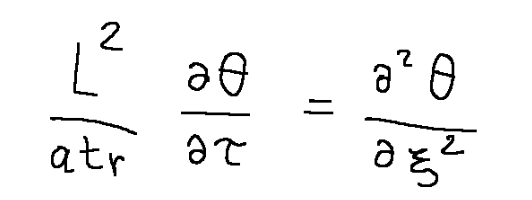
Ora vediamo come diventano sia la condizione iniziale che che condizioni al contorno.
Condizione iniziale semplificata
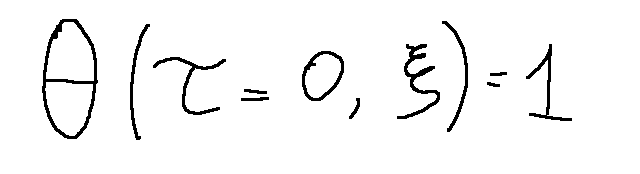
Condizioni al contorno semplificate
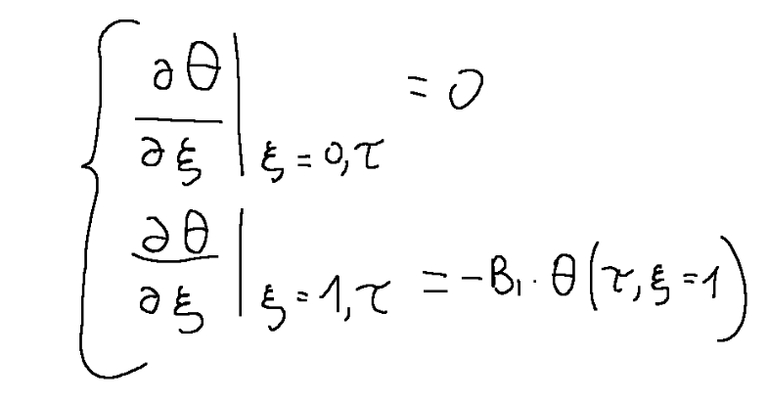
Notiamo in queste ultime equazioni il termine Bi
Questo è chiamato il numero di Biot che è il rapporto tra la resistività conduttiva (all′interno della lastra) fratto la resistività convettiva (all′esterno della lastra).
Il numero di Biot è un gruppo adimensionale usato principalmente nell'ambito della fluidodinamica.
Il nome deriva dal fisico francese Jean-Baptiste Biot vissuto tra la fine del 1700 e la prima metà del 1800.
Se Bi assume valori molto piccoli notiamo che la temperatura non dipende dal particolare punto di osservazione all’interno della lastra, ma dipende solo dal tempo.
Avremo infine che la soluzione sarà la seguente:
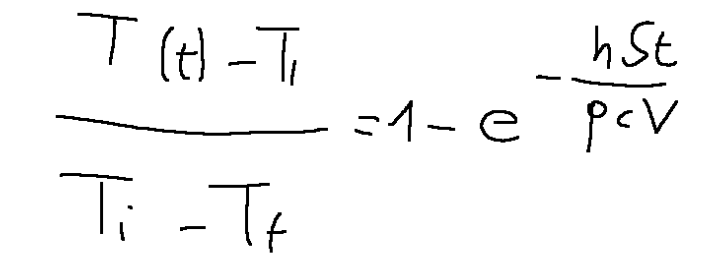
ed il diagramma si presenterà nella seguente maniera.

Conclusioni
Il numero di Biot è il rapporto tra la resistività conduttiva all'interno di una lastra e la resistività convettiva all'esterno di quella stessa lastra.
Domanda
Avete mai studiato la resistività conduttiva o la resistività convettiva?
THE END