
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

23-06-2025 - Mathematical Analysis - Functions[EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X-95)
Functions

image created with artificial intelligence, the software used is Microsoft Copilot
What is mathematical analysis used for
We can say that mathematical analysis is one of the most used tools in scientific subjects to understand change or movement.
Furthermore, mathematical analysis helps us to predict, through models, the spread of a disease, road traffic, or the variation of market prices.
Functions
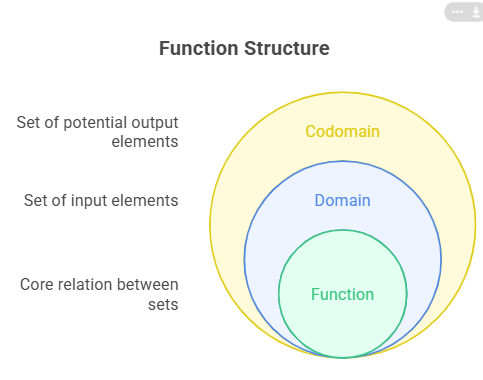
image created with artificial intelligence, the software used is Napkin.ai
In mathematical analysis, functions play an important role.
A function is a relation that associates each element of a set with a single element of another set.
The first set is called the domain, while the second set is called the codomain.
A function is indicated as follows:

This expression is read as follows: f defined from A to B
So we can say that a function f between two sets A and B is a law that associates one and only one element of B to each element A. In the expression described above we can say that A is called the domain of f and B is called the codomain of f.
Graph of the function
The graph of the function is a representation of the function in the Cartesian plane through the pairs (x, f(x)) considered for each x that belongs to A (x ∈ A).
Below is an example graph of a function graph.
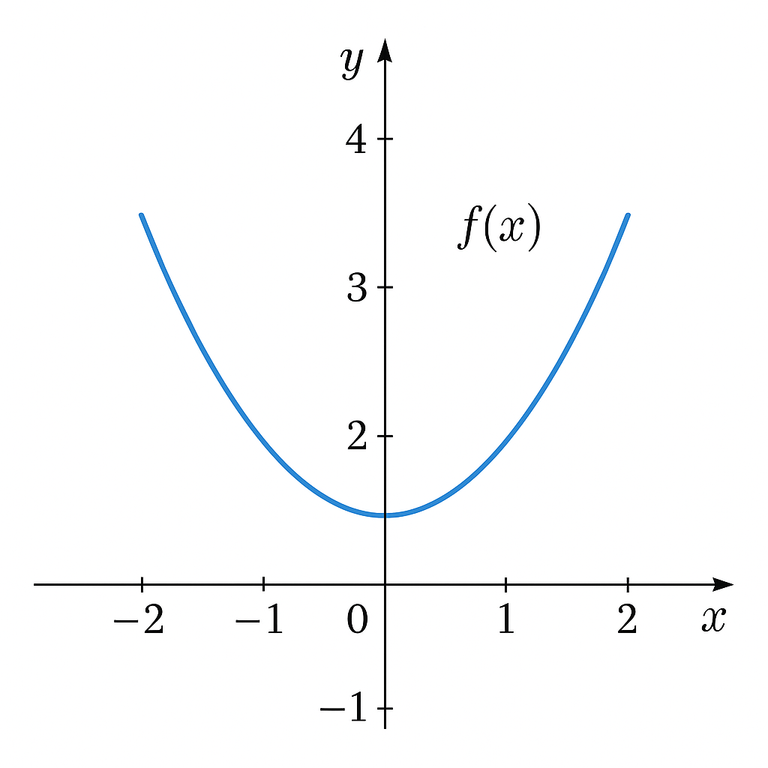
image created with artificial intelligence, the software used is ChatGPT
Types of functions
There are three types of functions: injective, surjective and bijective.
Injective
A function is said to be injective if it makes distinct elements of the domain correspond to distinct elements of the codomain.
Surjective
A function is surjective if the image f(A) coincides with B.
We can also say that a surjective function is a function in which every element of the codomain is the image of at least one element of the domain
Example
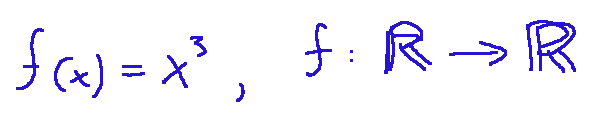
This is a surjective function because every real number has at least one real cube root.
Bijective
A bijective function is a function that is both injective and surjective. Bijective functions are also called biunivocal or bijective.
In simple terms, a bijective function establishes a one-to-one correspondence between the elements of the domain and those of the codomain.
That is, every element of x that belongs to A such that
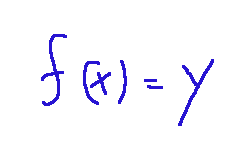
Bounded function
A function is said to be bounded above or below if its image is a set bounded above or below. A function is said to be bounded if it is bounded both above and below.
Mathematically, what we have just said is expressed like this
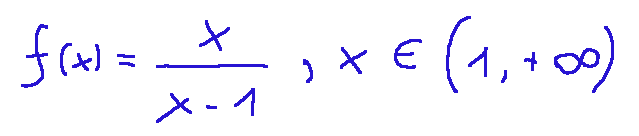
Conclusions
Mathematical analysis is used above all to study the physical world and understand it, it is also used to understand the behavior of complex functions
Question
Did you know that among the first scholars associated with the concept of function there is Sharaf al-Din al-Tusi, a Persian mathematician and astronomer (now IRAN) born in 1135 and died in 1213?

ITALIAN

23-06-2025 - Analisi Matematica - Le funzioni[EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-95)
Le funzioni

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
A cosa serve l'analisi matematica
Possiamo affermare che 'analisi matematica sia uno degli strumenti più usati nelle materie scientifiche per comprendere il cambiamento o il movimento.
Inoltre l'analisi matematica ci serve per prevedere, attraverso dei modelli, la diffusione di una malattia, il traffico stradale, oppure la variazione dei prezzi di mercato.
Le funzioni

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
In analisi matematica le funzioni svolgono un ruolo importante.
Una funzione è una relazione che associa a ogni elemento di un insieme un solo elemento di un altro insieme.
Il primo insieme è detto dominio, mentre il secondo insieme è detto codominio.
Una funzione si indica come segue:

Questa espressione si legge così: f definita da A a B
Quindi possiamo dire che una funzione f tra due insiemi A e B è una legge che ad ogni elemento A associa uno ed un solo elemento di B. Nell'espressione sopra descritta possiamo dire che A è detto dominio di f e B è detto codominio di f.
Grafico della funzione
Il grafico della funzione si tratta di una rappresentazione della funzione nel piano cartesiano attraverso le coppie (x, f(x)) considerate per ogni x che appartiene ad A (x ∈ A).
Qui di seguito un grafico d'esempio di un grafico di una funzione.

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Le tipologie delle funzioni
Le funzioni sono di tre tipologie: iniettive, suriettive e biiettive.
Iniettive
Una funzione si dice iniettiva se ad elementi distinti del dominio fa corrispondere distinti elementi del codominio.
Suriettiva
Una funzione è suriettiva se l'immagine f(A) coincide con B.
Possiamo anche dire che una funzione suriettiva è una funzione in cui ogni elemento del codominio è immagine di almeno un elemento del dominio
Esempio
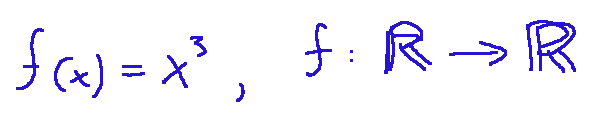
Questa è una funzione suriettiva perché ogni numero reale ha almeno una radice cubica reale.
Biiettiva
Una funzione biiettiva è una funzione che è sia iniettiva che suriettiva. Le funzioni biiettive sono dette anche biunivoche o bigettive.
In parole semplici una funzione biiettiva stabilisce una corrispondenza uno a uno tra gli elementi del dominio e quelli del codominio.
Cioè, ogni elemento di x che appartiene ad A in modo tale che
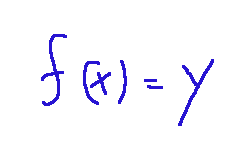
Funzione superiormente o inferiormente limitata
Una funzione si dice superiormente o inferiormente limitata se la sua immagine è un insieme superiormente o inferiormente limitato. Si dice che una funzione è limitata se essa è limitata sia superiormente che inferiormente.
Matematicamente ciò che abbiamo appena detto si esprime così
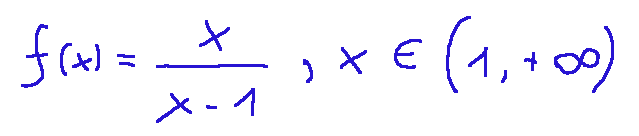
Conclusioni
L'analisi matematica è usata soprattutto per studiare il mondo fisico e comprenderlo, inoltre serve per comprendere il comportamento di funzioni complesse
Domanda
Lo sapevate che tra i primi studiosi associati al concetto di funzione c'è Sharaf al‑Din al‑Tusi, matematico e astronomo persiano (attuale IRAN) nato nel 1135 e morto nel 1213?
THE END
