
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
04-02-2025 - Analytic geometry - Gaussian elimination [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_88)
Gaussian Elimination
First of all let's talk about elementary operations
One of the elementary operations is called type I operation
The type I operation is the exchange of two rows of a given matrix A;
Example
Let's see an elementary operation on type I rows that swaps the second and third rows
Given the following matrix:
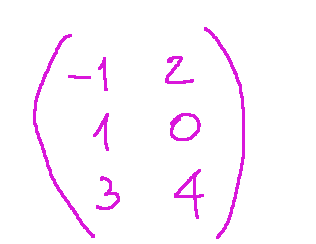
Swap row 2 with row 3
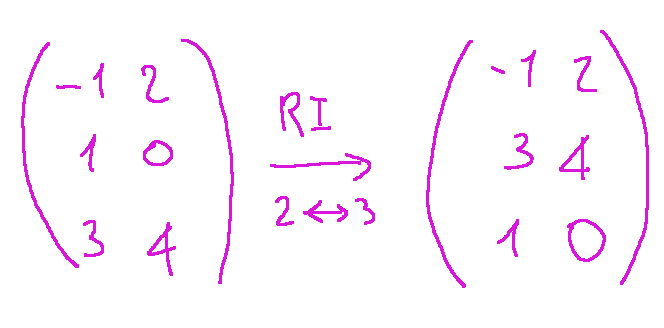
In case it wasn't clear, what we did is represented below graphically.
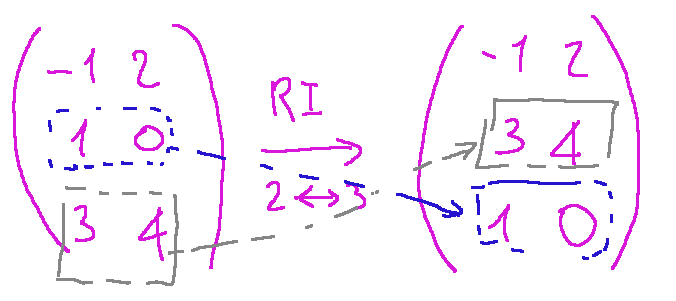
Gaussian Elimination Method
Here is an example of how to apply the Gaussian Elimination Method
Let's take the following matrix as an example
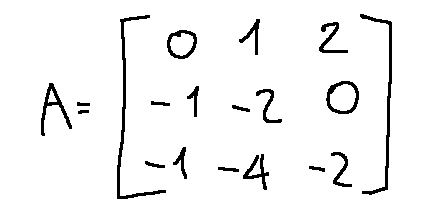
Step 1
Swap rows to get a non-null pivot
The first element (0,1) is 0, so we swap the first row with the second to get a non-null pivot:
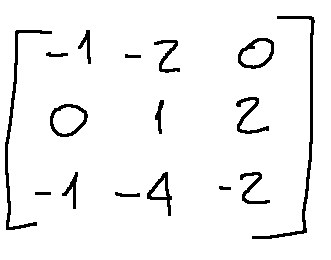
Step 2
Remove the term under the pivot
To cancel the -1 in position (3,1), we do the following operation R3 = R3-R1
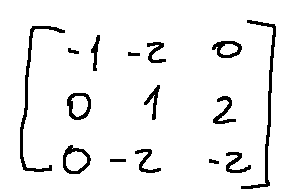
Step 3
Eliminating the term under the second pivot
We have 1 in position (2,2), so we can eliminate the -2 in position (3,2) by doing R3 = R3 + 2R2
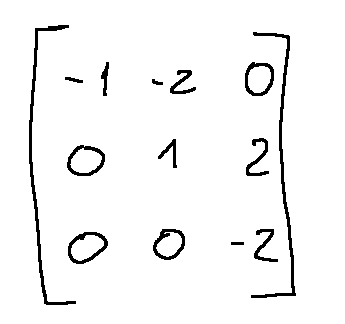
Considerations
Using the Gaussian elimination method we will obtain that, after the row operations (swap, multiplication, addition/subtraction of rows), the matrix will assume the following shape:
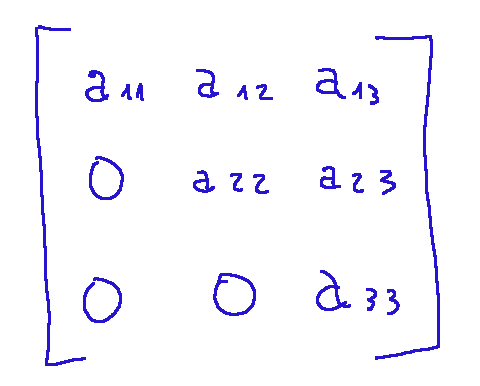
Conclusions
The Gaussian elimination method applied to matrices is used to transform a linear system into a simpler form, allowing us to easily find solutions. In particular, it allows us to obtain an upper triangular matrix, that is, a matrix in which all the elements under the main diagonal are zeros.
Question
Have you ever heard of the Gaussian elimination method applied to matrices?

[ITALIAN]
04-02-2025 - Geometria analitica - eliminazione di Gauss [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_88)
Eliminazione di Gauss
Innanzitutto parliamo delle operazioni elementari
Una delle operazioni elementari è definita operazione di tipo I
L'operazione di tipo I è scambio di due righe di una determinata matrice A;
Esempio
Vediamo un'operazione elementare sulle righe di tipo I che scambia la seconda e la terza riga
Data seguente matrice:
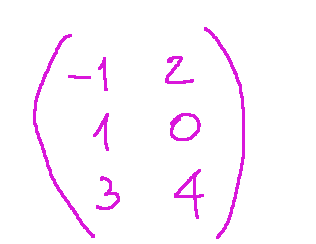
Scambiamo la riga 2 con la 3
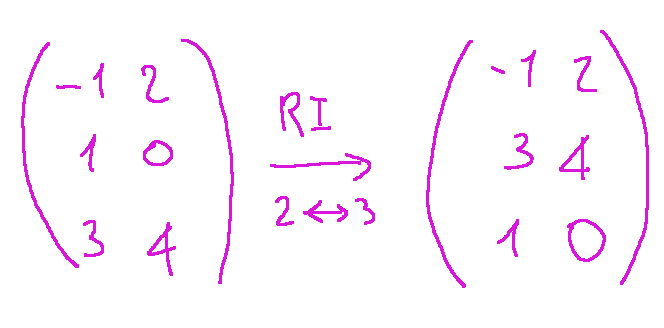
Se non fosse chiaro, quello che abbiamo fatto è rappresentato qui di seguito graficamente.

Metodo dell'eliminazione di Gauss
Qui di seguito un esempio di come si applica il metodo dell'eliminazione di Gauss
Prendiamo come esempio la seguente matrice
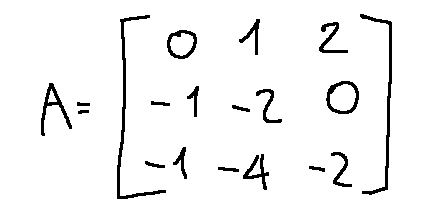
Passo 1
Scambio di righe per ottenere un pivot non nullo
Il primo elemento (0,1) è 0, quindi scambiamo la prima riga con la seconda per ottenere un pivot non nullo:
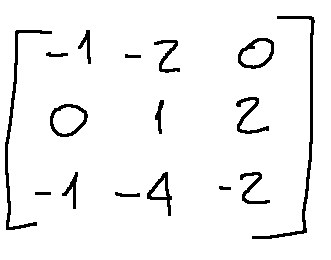
Passo 2
Eliminazione del termine sotto il pivot
Per annullare il -1 in posizione (3,1), facciamo la seguente operazione R3 = R3-R1
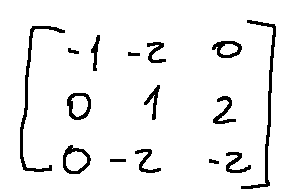
Passo 3
Eliminazione del termine sotto il secondo pivot
Abbiamo 1 in posizione (2,2), quindi possiamo eliminare il -2 in posizione (3,2) facendo R3 = R3 + 2R2

Considerazioni
Usando il metodo di eliminazione di Gauss otterremo che, dopo le operazioni di riga (scambio, moltiplicazione, somma/sottrazione di righe), la matrice assumerà la seguente forma:
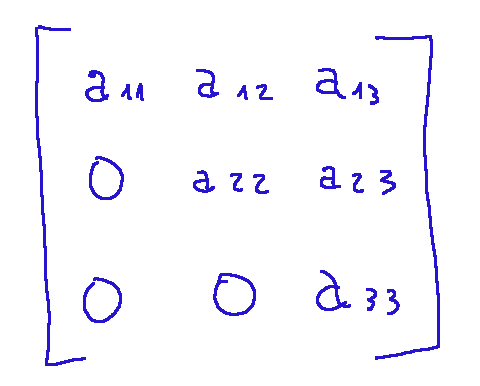
Conclusioni
Il metodo di eliminazione di Gauss applicato alle matrici serve a trasformare un sistema lineare in una forma più semplice, permettendo di trovare facilmente le soluzioni. In particolare, ci consente di ottenere una matrice triangolare superiore, ovvero una matrice in cui tutti gli elementi sotto la diagonale principale sono zeri.
Domanda
Avete mai sentito parlare del metodo di eliminazione di Gauss applicato alle matrici?
THE END
