~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
02-12-2024 - Analytic Geometry - Quadrics [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_53)
Quadrics
What are they
Quadrics are algebraic surfaces of degree two and almost all the ideas about conics can be generalized to quadrics.
Definition
A quadratic is an algebraic surface of degree 2, that is, it is the set of points that satisfy a polynomial equation p(x,y,z)=0 of degree 2.
For example, spheres, cones and cylinders are quadratics of degree 2.
A pair of planes is a quadratic. In fact, its equation
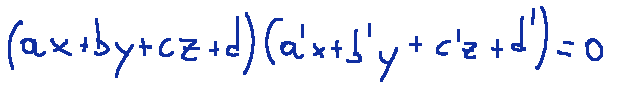
is a polynomial equation of degree 2.
Observation
The homogeneous equation of a quadratic can be thought of as a quadratic form.
The matrix associated with it is a 4 x 4 symmetric matrix A such that
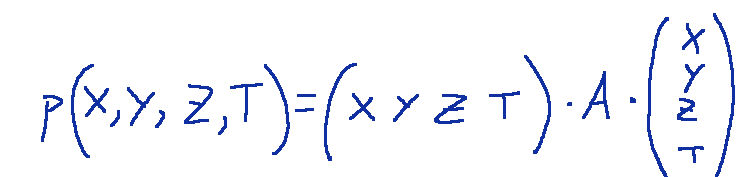
Further definition
Given a quadratic S with homogeneous equation
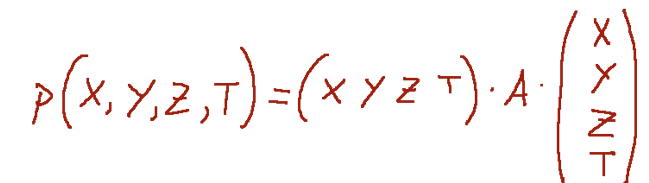
with the notation of the previous observation, the matrix A is called matrix associated with the quadratic S.
Degenerate Quadratics
A quadratic with associated matrix A is said to be degenerate if the determinant of A is equal to 0.
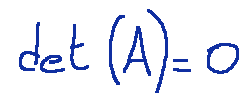
Euclidean classification of quadrics
A non-degenerate quadric S with associated matrix A can be represented by one of the following Euclidean canonical forms with an appropriate choice of the Cartesian reference system.
Below are their algebraic representations.
-real ellipsoid
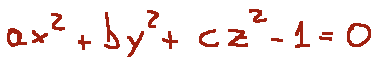
-imaginary ellipsoid
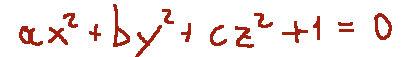
-hyperboloid elliptical

-hyperbolic hyperboloid
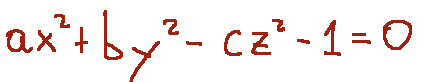
-paraboloid elliptic
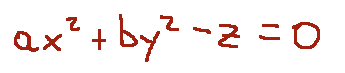
-hyperbolic paraboloid
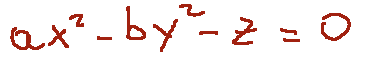
Conclusions
In analytical geometry, quadrics are second-degree algebraic surfaces in three-dimensional space (ℝ³), described by a general equation written as follows:
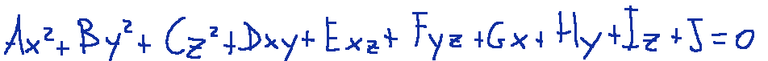
Question
In my opinion, quadrics are a little-known topic in the study world and are a fairly complex part of analytical geometry, do you also think so or not?

[ITALIAN]
02-12-2024 - Geometria analitica - Quadriche [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_53)
Le quadriche
Cosa sono
le quadriche sono superfici algebriche di grado due e quasi tutte le idee sulle coniche possono essere generalizzate alle quadriche.
Definizione
Una quadratica è una superficie algebrica di grado 2, ossia è l’insieme dei punti che soddisfano un’equazione polinomiale p(x,y,z)=0 di grado 2.
Ad esempio le sfere, i coni ed i cilindri sono quadratiche di grado 2.
Una coppia di piani è una quadratica. Infatti la sua equazione
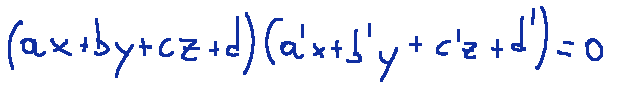
è un'equazione polinomiale di grado 2.
Osservazione
L’equazione omogenea di una quadratica può essere pensata come una forma quadratica.
La matrice associata ad essa è una matrice 4 x 4 simmetrica A tale che
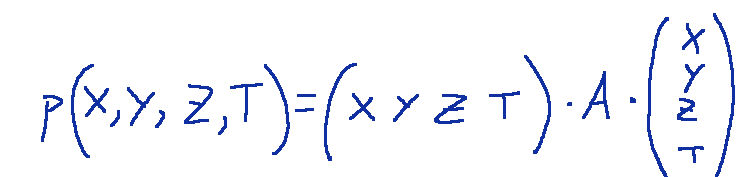
Definizione ulteriore
Data una quadratica S con equazione omogenea
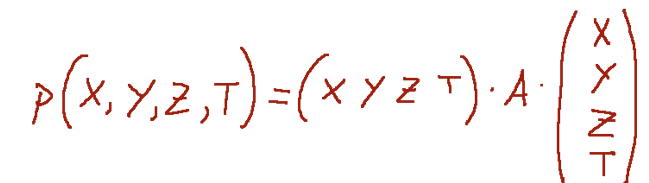
con la notazione della precedente osservazione, la matrice A è detta matrice associata alla quadratica S.
Quadratiche degeneri
Una quadratica con matrice associata A è detta degenere se il determinante di A è uguale a 0.
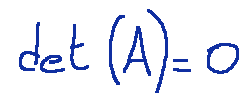
Classificazione euclidea delle quadriche
Una quadrica non degenere S con matrice associata A può essere rappresentata da una delle seguenti forme canoniche euclidee con una scelta opportuna del sistema di riferimento cartesiano.
Qui di seguito le loro rappresentazioni algebriche.
-ellissoide reale
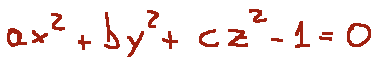
-ellissoide immaginario
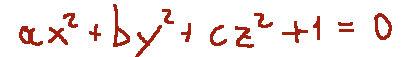
-iperboloide ellittico

-iperboloide iperbolico
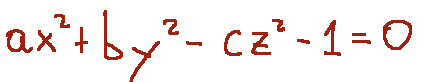
-paraboloide ellittico
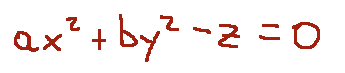
-paraboloide iperbolico
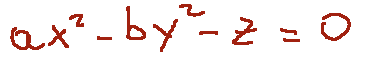
Conclusioni
In geometria analitica, le quadriche sono superfici algebriche di secondo grado nello spazio tridimensionale (ℝ³), descritte da un'equazione generale scritta come segue:
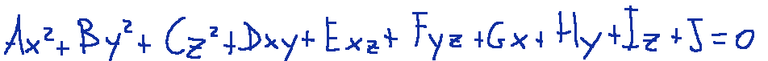
Domanda
Secondo me, le quadriche sono un argomento poco diffuso nel mondo dello studio e sono una parte della geometria analitica abbastanza complessa, anche secondo voi è così oppure no?
THE END




