
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

26-03-2025 - Chemistry Basics - Thermodynamics (part 7) [EN]-[IT]
With this post I would like to give a brief instruction on the topic mentioned in the subject
(code notes: X_66)
Thermodynamics (part 7)
Let's start from the fact that we have learned the concept expressed by the state entropy function S according to Boltzmann's definition (S=kBlnW) in which W represents the number of possible ways at a "microscopic" level (called "microstates") in which a certain thermodynamic state can be obtained. This relationship also contemplates the case in which W=1 which implies that S is zero. In essence, it is possible that there exists a thermodynamic state characterized by a perfect order (W=1). This is essentially the concept expressed by the 3rd Law of Thermodynamics. It states that at absolute zero (T=0 K) the entropy of a perfect crystal is zero.
This is also known as Nernst's Theorem.
3rd Law of Thermodynamics
The third law of thermodynamics states that the entropy of a perfect crystal tends to zero when the temperature approaches absolute zero, that is, 0 K. We can also essentially say that when a system reaches the state of perfect order, there is no more molecular disorder and at this point the entropy is zero. Trying to make the fundamental concept of the third law of thermodynamics even better understood, we can say that this principle states that at 0 K the disorder is minimal and the entropy is completely eliminated.
Arrangement of crystals and 3rd law
Let's imagine cooling the element neon, which at room temperature is a noble gas. As the temperature decreases we can imagine that the movements of the Ne atoms become slower and slower and that the atoms themselves get closer and closer to each other. Even at the temperature of 27.07 K (-246.08 °C) the Ne passes to the liquid state while at 24.56 K (-248.59 °C) it becomes solid. During all these transformations we expect a significant increase in order of the system or a significant reduction in entropy. Even if the temperature of 0 K cannot actually be reached, it is possible, with appropriate techniques, to reach temperatures very close to it. It is reasonable to expect that at such low temperatures the Ne atoms are not only regularly packed in an ordered crystalline lattice but that any vibration of them around the equilibrium positions is precluded. Therefore it can be assumed that in the limit for T tending to 0 K, there is only one microstate, that is, W=1.
Here is a diagram of what was said above:
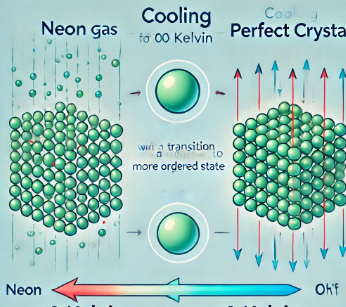
Image generated with AI, ChatGPT software
From the image above we can see that the lower the temperature, the more the Ne atoms are regularly arranged in an ordered crystal lattice.
Below I try to describe what happens to neon when going from a higher temperature to a lower one, then trying to lower the temperature as close as possible to absolute zero.
We divide the process into three parts where the first part is the situation with the highest temperature
-1-
At high temperatures, such as 300 K, neon molecules move quickly in all directions. The level of disorder is high and entropy is high.
-2-
As the temperature decreases, the kinetic energy of the molecules decreases and the particles begin to organize themselves in a more orderly way
-3-
At 0 K, the molecules align perfectly in the ideal crystal, reaching a maximum order and therefore the entropy of the system is zero
NOTE: Absolute zero is the lowest temperature theoretically possible, corresponding to 0 Kelvin (273.15∘C).
Entropy
We said that entropy at 0 K is zero, but what is its mathematical formula?
The entropy S is defined by the following relation:
dS=dQrev/T
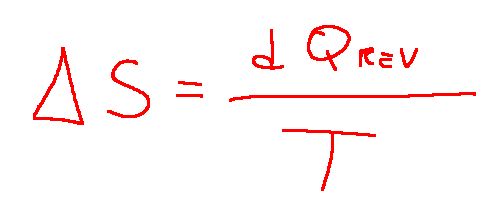
Conclusions
We can define the third law of thermodynamics as the final part of what could be a general explanation of thermodynamics. In summary, this principle states that At 0 K, the entropy of a perfect crystal is zero.
Question
Did you know that the closer we get to absolute zero, the more atoms and molecules arrange themselves in a regular and non-confusing way? Did you know that at absolute zero, entropy does not exist and atoms completely stop all vibrational motion?

ITALIAN

26-03-2025 - Basi di chimica - Termodinamica (parte 7) [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_66)
Termodinamica (parte 7)
Partiamo dal fatto di aver appreso il concetto espresso dalla funzione di stato entropia S secondo la definizione di Boltzmann (S=kBlnW) in cui W rappresenta il numero di possibili modi a livello “microscopico” (chiamati “microstati”) in cui un certo stato termodinamico può essere ottenuto. Tale relazione contempla anche il caso in cui W=1 che implica che S sia nulla. In sostanza è possibile che esista uno stato termodinamico caratterizzato da un ordine perfetto (W=1). È questo in sostanza il concetto espresso dal 3° Principio della Termodinamica. Esso afferma che allo zero assoluto (T=0 K) l’entropia di un cristallo perfetto è nulla.
Questo è noto anche come Teorema di Nernst.
3° Principio della Termodinamica
Il terzo principio della termodinamica definisce che l’entropia di un cristallo perfetto tende a zero quando la temperatura si avvicina allo zero assoluto, cioè a 0 K. Sostanzialmente possiamo dire anche che quando un sistema raggiunge lo stato di ordine perfetto non esiste più disordine molecolare e a questo punto l’entropia è nulla. Cercando di far capire ancora meglio il concetto fondamentale del terzo principio della termodinamica, possiamo dire che questo principio afferma che a 0 K il disordine è minimo e l’entropia si annulla completamente.
Disposizione dei cristalli e 3° principio
Immaginiamo di raffreddare l’elemento neon, che a temperatura ambiente è un gas nobile. Man mano che la temperatura si riduce possiamo immaginare che i movimenti degli atomi di Ne diventino sempre più lenti e che gli atomi stessi si avvicinino sempre di più tra di loro, Addirittura alla temperatura di 27.07 K (-246.08 °C) il Ne passa allo stato liquido mentre a 24.56 K (-248.59 °C) diventa solido. Durante tutte queste trasformazioni ci aspettiamo un significativo aumento di ordine del sistema ovvero una significativa riduzione dell’entropia. Anche se la temperatura di 0 K non può essere raggiunta effettivamente, è possibile, con opportune tecniche, arrivare a temperature molte prossime ad esso. È lecito attendersi che a così basse temperature gli atomi di Ne siano non solo regolarmente impaccati in un reticolo cristallino ordinato ma che sia preclusa ogni loro vibrazione intorno alle posizioni di equilibrio. Quindi si può ritenere che al limite per T che tenda a 0 K, esista un solo microstato, cioè che sia W=1.
Qui di seguito uno schema di quanto detto sopra:

Immagine generata con IA, software ChatGPT
Dall'immagine qui sopra riportata notiamo che più la temperatura si abbassa e più gli atomi di Ne sono regolarmente disposti in un reticolo cristallino ordinato.
Qui di seguito provo a descrivere cosa avviene al neon passando da una temperatura maggiore ad in inferiore, cercando poi di abbassare la temperatura più vicino possibile allo zero assoluto.
Dividiamo il processo in tre parti in cui la prima parte è la situazione con maggior temperatura
-1-
A temperature alte, tipo 300 K, le molecole di neon si muovono velocemente in tutte le direzioni. Il livello di disordine è alto e l'entropia è alta.
-2-
Man mano che la temperatura diminuisce, l'energia cinetica delle molecole diminuisce e le particelle iniziano a organizzarsi in modo più ordinato
-3-
A 0 K, le molecole si allineano perfettamente nel cristallo ideale, raggiungendo un massimo ordine e quindi l'entropia del sistema si annulla
NOTA: Lo zero assoluto è la temperatura più bassa teoricamente possibile, corrispondente a 0 Kelvin (273.15∘C).
L'entropia
Abbiamo detto che l'entropia a 0 K è nulla, ma quel è la sua formula matematica?
L'entropia S è definita mediante la seguente relazione:
dS=dQrev/T
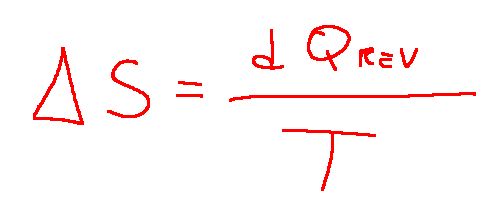
Conclusioni
Possiamo definire il terzo principio della termodinamica come la parte conclusiva di quella che potrebbe essere una spiegazione generale della termodinamica. In sintesi questo principio afferma che A 0 K, l'entropia di un cristallo perfetto è zero.
Domanda
Lo sapevate che più ci avviciniamo allo zero assoluto e più gli atomi e le molecole si dispongono in maniera regolare e non confusionaria? Lo sapevate che alla temperatura dello zero assoluto non esiste entropia e gli atomi interrompono completamente ogni movimento vibrazionale?
THE END
