
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
13-02-2025 - Analytical Geometry - Cramer[EN]-[IT]
With this post I would like to give a brief instruction on the topic mentioned in the subject
(code notes: X_74)
Cramer
When we deal with the subject of analytical geometry, at a certain point we come across Cramer.
Gabriel Cramer was a Swiss mathematician (1704-1752) who in his book entitled "Introduction à l'Analyse des lignes courbes algébriques", published in 1750, presented a rule, which is now known as "Cramer's rule"
Cramer's rule is a method used to solve systems of linear equations by calculating the determinants. It applies to square systems, that is, those in which the number of equations is equal to the number of unknowns.
NOTE: Cramer was the first to clearly and systematically formulate the method for solving systems of linear equations through the calculation of determinants. However, the method based on determinants was already known in some forms to previous mathematicians, such as Leibniz.
EXAMPLE
Below I will perform an example quickly, I will not go into the details of the individual transformations
Let's take for example the following system of linear equations.
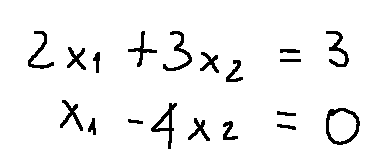
Now let's try to understand how much the coordinate x1 of the solution of the system of linear equations obtained by applying Cramer's rule is worth
Let's start!!
Step 1
-Let's immediately identify the coefficient matrix
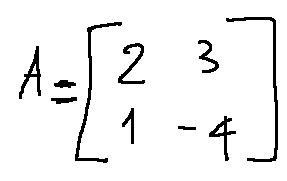
The vector of known terms is
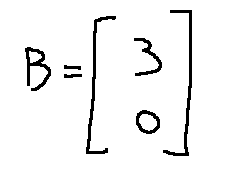
Step 2
and now we can calculate the determinant of A
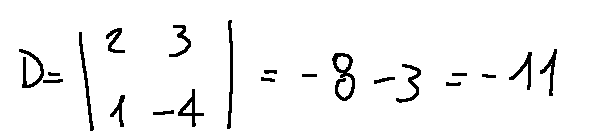
Step 3
Now let's build the matrix A1 by replacing the first column with the vector of known terms.
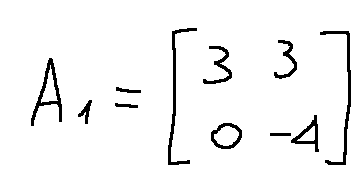
At this point we can know the determinant of A1 which will be...
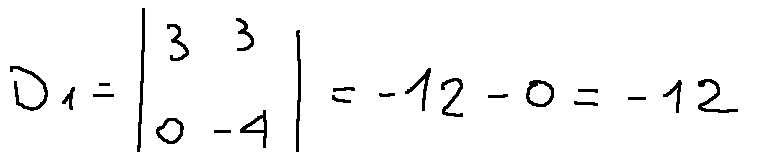
Step 4
Let's calculate x1 using the rule of Cramer
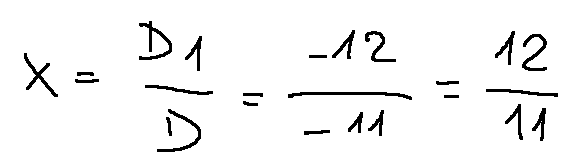
Final result
The x1 coordinate of the solution is 12/11
If we want, we can also say that the solution is
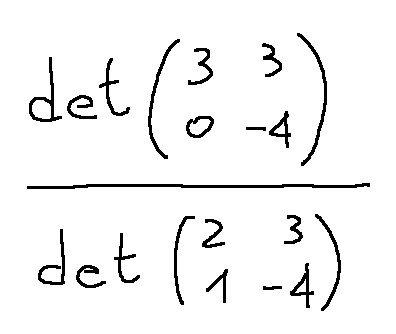
Conclusions
Cramer's rule is particularly useful for solving systems of small size, but for very large systems it becomes inefficient compared to other methods, such as Gauss's method.
Question
Have you ever heard of the Swiss mathematician Gabriel Cramer before? Do you remember studying him in school?

[ITALIAN]
13-02-2025 - Geometria analitica - Cramer[EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_74)
Cramer
Quando affrontiamo la materia geometria analitica, ad un certo punto ci imbattiamo in Cramer.
Gabriel Cramer fu un matematico svizzero (1704-1752)che nel suo libro intitolato "Introduction à l'Analyse des lignes courbes algébriques", pubblicato nel 1750, presentò una regola, quella che oggi è nota come "La regola di Cramer"
La regola di Cramer è un metodo utilizzato per risolvere sistemi di equazioni lineari mediante il calcolo dei determinanti. Si applica a sistemi quadrati, cioè quelli in cui il numero di equazioni è uguale al numero di incognite.
NOTA: Cramer fu il primo a formulare in modo chiaro e sistematico il metodo per risolvere sistemi di equazioni lineari attraverso il calcolo dei determinanti. Tuttavia il metodo basato sui determinanti era già noto in alcune forme a matematici precedenti, come Leibniz.
ESEMPIO
Qui di seguito eseguo un esempio in maniera veloce, non entrerò nei dettagli delle singole trasformazioni
Prendiamo per esempio il seguente sistema di equazioni lineari.
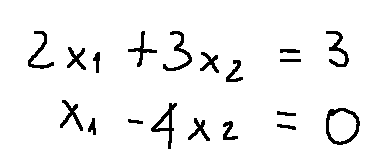
Ora proviamo di capire quanto vale la coordinata x1 della soluzione del sistema di equazioni lineari ottenuta applicando la regola di Cramer
Iniziamo!!
Passo 1
-Individuiamo subito la matrice dei coefficienti
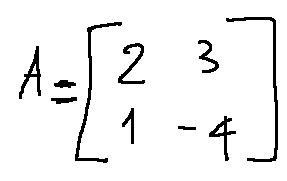
Il vettore dei termini noti è
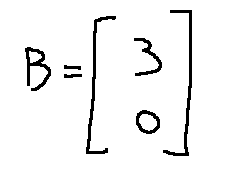
Passo 2
ed ora possiamo calcolare il determinante di A
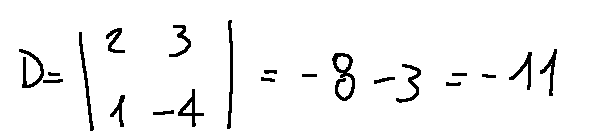
Passo 3
Costruiamo ora la matrice A1 sostituendo la prima colonna con il vettore dei termini noti.
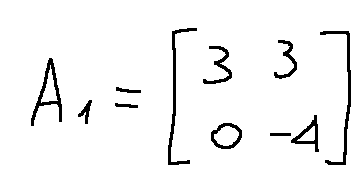
A questo punto possiamo conoscere il determinante di A1 che sarà...
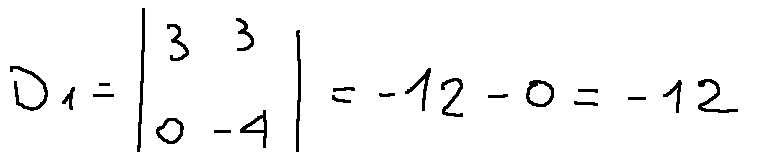
Passo 4
Calcoliamo x1 usando la regola di Cramer
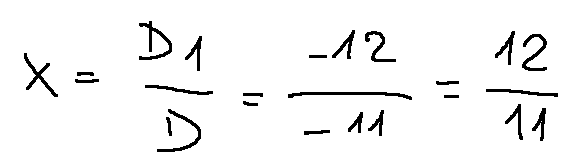
Risultato finale
La coordinata x1 della soluzione è 12/11
Volendo possiamo anche dire che la soluzione è
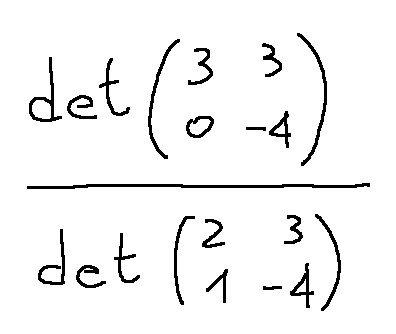
Conclusioni
La regola di Cramer è particolarmente utile per risolvere sistemi di piccole dimensioni, ma per sistemi molto grandi diventa inefficiente rispetto ad altri metodi, come il metodo di Gauss.
Domanda
Avevate mai sentito parlare prima d'ora del matematico svizzero Gabriel Cramer? Ricordate di averlo studiato a scuola?
THE END