
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

29-06-2025 - Mathematical Analysis - Complex Numbers [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-89)
Complex Numbers

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Complex numbers were created to make sense of some algebraic operations that are impossible in the set of real numbers.
A classic example is the square root of a negative number.
With the advent of quantum mechanics, complex numbers have become fundamental for the formulas described in that field.
Complex numbers help to better describe electrical circuits, electromagnetic fields and signal transmissions.
Working or studying in certain situations with complex numbers is easier.
Below is an example that explains the need for using complex numbers, or rather, what can be described using a complex number that otherwise could not be described.
Consider the following equation:

This equation has no solutions in...
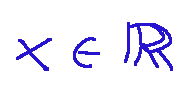
that is, it has no solutions if x is any real number.
but we can define the following:
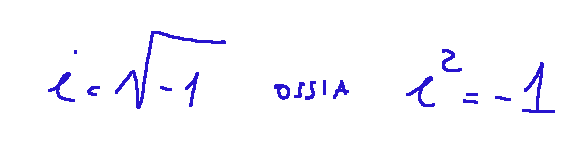
If instead we enter the set of complex numbers then things change.
and we have the following solutions, solutions defined in the context of complex numbers.
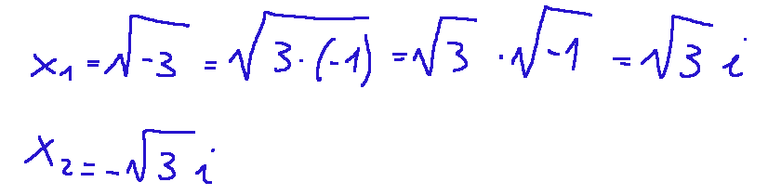
The set of complex numbers is usually denoted by the letter C.

A complex number has the general formula following:
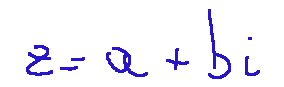
Where:
a and b belong to the set of real numbers
i is the imaginary unit, defined by i^2 = -1
We can say what the above formula means using the following words. A complex number z is defined as the sum of a real number a and a real multiple b of i.
Example
Shall we consider this term?
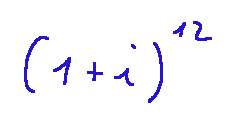
Now let's try to understand how much the real part is worth:
the first observation to make is the following:
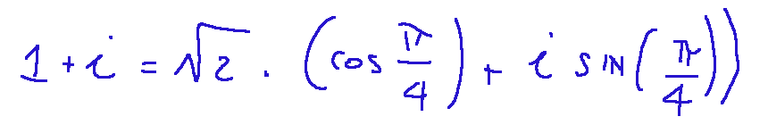
Note: to do these exercises with complex numbers it is necessary to remember the De Moivre formula that I report here below:
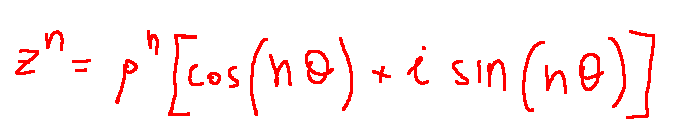
Now let's proceed with the transformations to arrive at the conclusion of the exercise proposed above.
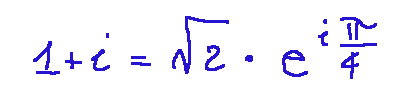
raising to the twelfth we will have:
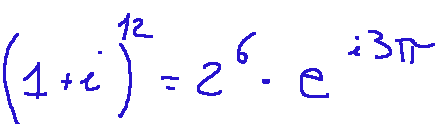
continuing with the transformations we arrive at solution
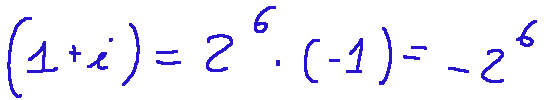
so the real part of...
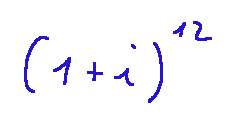
it is...
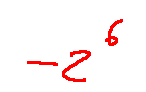
Conclusions
Complex numbers are used to manage concepts and formulas that real numbers could not handle. Complex numbers are fundamental in the field of electrical engineering, quantum physics and also graphics and animation. They essentially expand the capabilities of mathematics even further.
Question
Did you know that one of the most famous people in the field of the study of complex numbers was the French mathematician Abraham de Moivre (1667-1754)? According to a legend, at a certain point in his life, De Moivre noticed that he slept a few minutes more every day, and continuing like this he calculated that he would sleep 24 hours on November 27, 1754, the exact day he died. Did you know the legend of De Moivre?

ITALIAN

29-06-2025 - Analisi Matematica - I numeri complessi [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-89)
I numeri complessi

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
I numeri complessi vennero creati per dare un senso ad alcune operazioni algebriche impossibili nell'insieme dei numeri reali.
Un classico esempio è la radice quadrata di un numero negativo.
Con l'avvento della meccanica quantistica i numeri complessi sono diventati fondamentale per le formule descritte in quell'ambito.
I numeri complessi aiutano a descrivere meglio i circuiti elettrici, i campi elettromagnetici e le trasmissioni di segnali.
Lavorare o studiare in certe situazioni con i numeri complessi risulta più semplice.
Qui di seguito un esempio che spiega la necessità dell'uso dei numeri complessi, o meglio, cosa si può descrivere usando un numero complesso che altrimenti non si potrebbe descrivere.
Consideriamo l'equazione seguente:

Questa equazioni non ha soluzioni in...
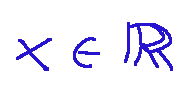
cioè non ha soluzioni se x è un qualunque numero reale.
però possiamo definire quanto segue:
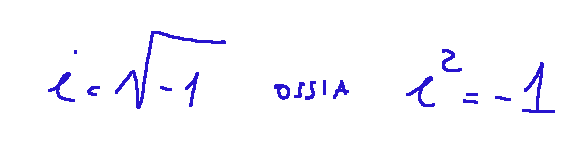
Se invece entriamo nell'insieme dei numeri complessi allora le cose cambiano.
e si hanno le soluzioni seguenti, soluzioni definite nell'ambito dei numeri complessi.
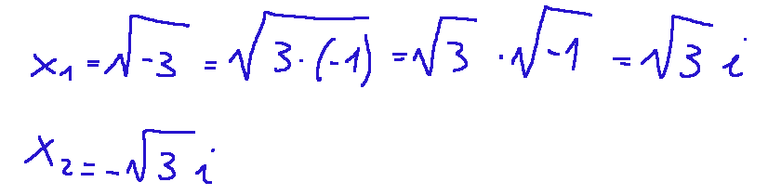
L'insieme dei numeri complessi è solitamente indicato con la lettera C.

Un numero complesso ha la formula generale seguente:
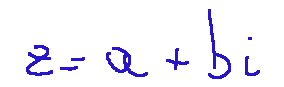
Dove:
a e b appartengono all'insieme dei numeri reali
i è l'unità immaginaria, definita da i^2 = -1
Possiamo dire cosa significa la formula sopra usando le seguenti parole. Un numero complesso z è definito come la somma di un numero reale a e di un numero multiplo reale b di i.
Esempio
Prendiamo in considerazione questo termine?
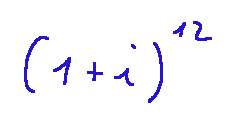
proviamo ora a capire quanto vale la parte reale:
la prima osservazione da fare è la seguente:
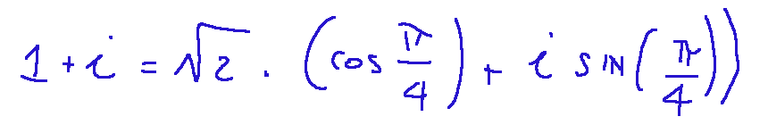
Nota: per fare questi esercizi con in numeri complessi è necessario ricordare la formula di De Moivre che riporto qui sotto:
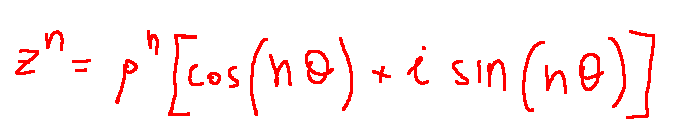
Ora procediamo con le trasformazioni per arrivare alla conclusione dell'esercizio proposto sopra.
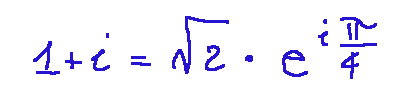
elevando alla dodicesima avremo:
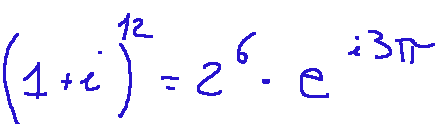
proseguendo con le trasformazioni arriviamo alla soluzione
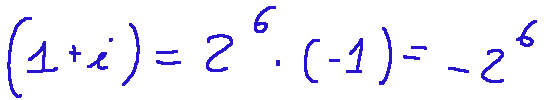
quindi la parte reale di...
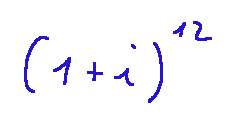
vale...
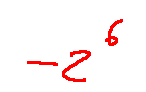
Conclusioni
I numeri complessi servono per gestire concetti e formule che con i numeri reali non si potrebbero maneggiare. I numeri complessi sono fondamentali nel campo dell'ingegneria elettrica, della fisica quantistica e anche della grafica e dell'animazione. Sostanzialmente ampliano ancora di più le capacità della matematica.
Domanda
Lo sapevate che una delle persone più celebri nell'ambito dello studio dei numeri complessi fu il matematico francese Abraham de Moivre (1667-1754)? Secondo una leggenda, ad un certo punto della sua vita, De Moivre si accorse che dormiva ogni giorno qualche minuto in più, e continuando così aveva calcolato che avrebbe dormito 24 ore il 27 novembre 1754, giorno esatto in cui morì. La conoscevate la leggenda di De Moivre?
THE END


