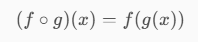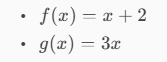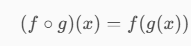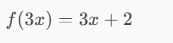~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

25-06-2025 - Mathematical Analysis - Composite and Inverse Functions [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X-93)
Composite and Inverse Functions

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
We can say that composite functions and inverse functions are two key concepts of mathematical analysis.
Composite Functions
Let's assume we have the following two functions:

Definition of a composite function
Let these two functions be such that the image of A is contained in the domain of g, Meaning what...
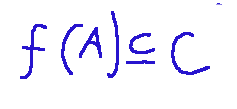
It is defined as a function composed of f and g la function...
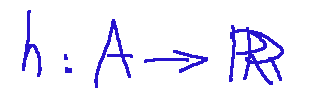
...defined...
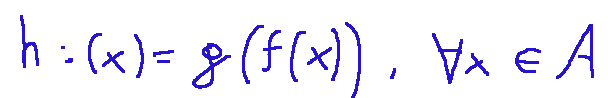
and you can also write so...

We can also show it differently and say that the composite function g or f is defined in the following way:
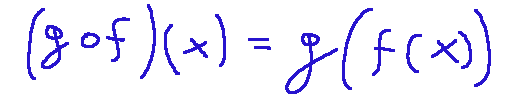
This means applying f to x and then subsequently applying g to the result of f(x)
example
let's think to have the following two functions:
f(x) = 2x
g(x) = x^2
We can have the composite function (g or f)(x), see example below for better understanding:

Inverse functions
The definition of an inverse function is as follows.
An inverse function, very simply, is a function that cancels the effect of another function. More precisely, if a function f takes a number x and returns y, its inverse takes the value of y and returns it to x.
Below is how a function is written on the left, while on the right is how its inverse is written.
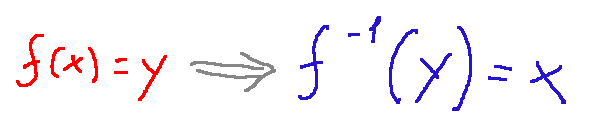
Example of an inverse function
Suppose we have the following function
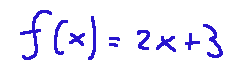
Let's try to calculate it for the value of x = 4

Essentially the inverse function tells us from which x the value 11 comes
It is in fact solved in the following way:
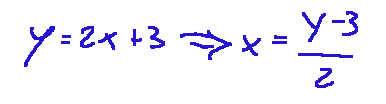
So the inverse function would be the following:

and if we apply 11 to this function, we will see that we will get the result 4, the data of the x that we had at the start or in other words the original input.
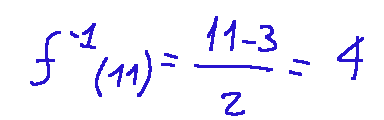
Conclusions
Composite functions allow you to apply multiple transformations one after the other and are essential for modeling multi-phase processes.
Inverse functions are studied when we need an inverse that “cancels” the effect of a function. In physics they are used to invert cause-effect relationships.
Question
Did you know that the systematic study of inverse functions spread with Leibniz, Euler and Lagrange? Did you know that Lagrange, the Italian mathematician naturalized French, used inverse functions to solve algebraic equations? And finally!! Did you know that the principle of inverse functions is the same principle that also applies in computer science and cryptography?

ITALIAN

25-06-2025 - Analisi Matematica - Funzioni composte e inverse [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-93)
Funzioni composte e inverse

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Possiamo dire che le funzioni composte e le funzioni inverse sono due concetti chiave dell'analisi matematica.
Funzioni composte
Pensiamo di avere le due seguenti funzioni:

Definizione di funzione composta
Siano queste due funzioni tali che l'immagine di A sia contenuta del dominio di g, cioè...
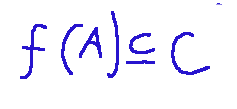
Si definisce funzione composta da f e g la funzione...
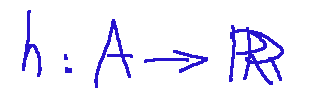
...definita...
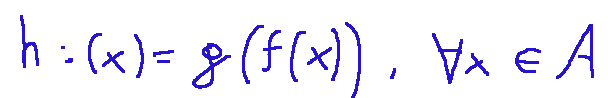
e si può scrivere anche così...

Possiamo anche mostrarlo in maniera diversa e dire che la funzione composta g o f si definisce nella seguente maniera:
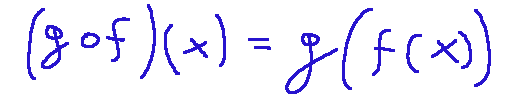
Questo significa applicare f a x e poi applicare successivamente g al risultato di f(x)
esempio
pensiamo di avere le due seguenti funzioni:
f(x) = 2x
g(x) = x^2
Possiamo avere la funzione composta (g o f)(x), vedi esempio qui sotto per maggior comprensione:

Funzioni inverse
La definizione di funzione inversa è la seguente.
Una funzione inversa, molto semplicemente, è una funzione che annulla l'effetto di un altra funzione. Più precisamente se una funzione f prende un numero x e restituisce y, la sua inversa prende il valore di y e lo riporta a x.
Qui di seguito è rappresentata la scrittura di una funzione a sinistra, mentre a destra è come si scrive la sua inversa.
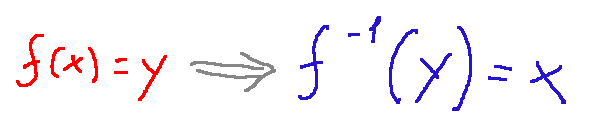
Esempio di una funzione inversa
Supponiamo di avere la seguente funzione
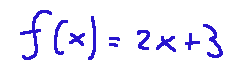
Proviamo a calcolarla per il valore di x = 4

Sostanzialmente la funzione inversa ci indica da quale x proviene il valore 11
Si risolve infatti nella seguente maniera:
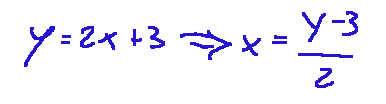
Quindi la funzione inversa sarebbe la seguente:

e se a questa funzione applichiamo 11, vedremo che otterremo il risultato 4, il dato della x che avevamo in partenza o in altre parole l'input originale.
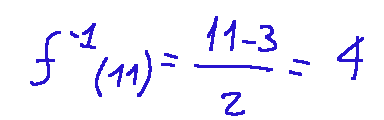
Conclusioni
Le funzioni composte permettono di applicare più trasformazioni una dopo l'altra e sono fondamentali per modellare processi in più fasi.
Le funzioni inverse si studiano quando abbiamo bisogno di un’inversa che “annulla” l’effetto di una funzione. In fisica vengono usate per invertire relazioni causa-effetto.
Domanda
Lo sapevate che lo studio sistematico delle funzioni inverse si diffusero con Leibniz, Euler e Lagrange? Lo sapevate che Lagrange, il matematico italiano naturalizzato francese, utilizzava le funzioni inverse per risolvere equazioni algebriche? Ed infine!! Lo sapevate che il principio delle funzioni inverse è lo stesso principio che vale anche in informatica e crittografia?
THE END