
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

25-04-2025 - Physics - Interactions between electric charges and potential [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_48-47-46-45)
Interactions between electric charges and potential

image created with artificial intelligence, the software used is Microsoft Copilot
The motion of electric charges
First of all let's define a concept that is that of the lines of force of an electric field now.
These are graphical representations that show the direction and intensity of the electric field in a region of space. The characteristics of the lines of force of an electric field are listed below:
Direction
Intensity
Tangent rule
Closed or open lines
Now let's better define the importance of the motion of electric charges. What is the motion of electric charges? We can say that this is the heart of everything that has to do with electric current. What is defined as the motion of electric charges in physics is simply the movement of electric charges within a material. When we talk about the motion of electric charges, we are simply and essentially talking about the very famous electric current.
The motion of the dipole
Without going too deep into the concept of the motion of the electric dipole, I simply write that it refers to the movement of an electric dipole (described in the previous post) under the action of an external electric field. Why is this concept important? Because in such a system the electric dipole can be subject to translation. That is, if the dipole is immersed in a uniform electric field, it will experience a net force that can make it move linearly in space.
Gauss's theorem
Gauss's theorem is one of the main theorems of electric fields and when we talk about this theorem it is good to know what the electric field flux is. This is a measure of the amount of electric field that passes through a surface. It is considered a fundamental quantity in electromagnetism. Gauss's law and one of Maxwell's equations best describe the electric field flux.
Technical definition
Gauss's theorem states that the flux of the electrostatic field in a vacuum E0, through any closed surface S is equal to the algebraic sum (or the integral in the case of continuous distribution) of the charges contained within S, divided by ε0.
Simplified definition
Gauss' theorem, in simple terms, we can say that it states that the amount of electric field that comes out of a closed surface depends only on how much charge is inside.
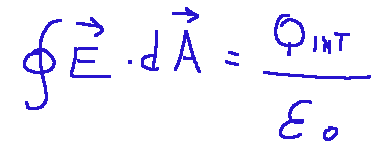
formula of Gauss's theorem
∮𝐸⋅𝑑𝐴 = flux of the electric field through a closed surface
Q int = total charge inside the surface
ε0 = constant called permittivity of vacuum
Maxwell's first equation
Gauss's theorem and Maxwell's first equation are essentially the same thing. We can say that Gauss's theorem was born as a principle of electrostatics while Max's first equation generalizes this theorem and inserts it into a much broader context which is that of the system of Maxwell's equations. The latter describe all electromagnetism.
Uniform distributions
Within the topic of electric fields, when we talk about uniform distributions, we are going to define something very specific. What is a uniform distribution? It occurs when a certain physical quantity is distributed in a constant way along a length, surface or volume. So if we talk about electric charges, a uniform distribution specifies that this electric charge is distributed in a regular way on the object we are studying.
The uniform distribution can also be spherical.
Electrostatic potential
The electric potential and the electrostatic potential are more or less the same thing. We talk about electrostatic potential when we are in the case of electrostatics, that is, with stationary charges and static electric fields. Recall that a static electric field is simply an electric field that does not change over time.
The formula for the Electrostatic Potential is as follows:
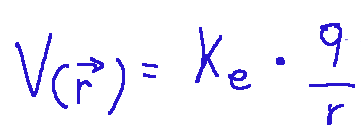
Where:
V( r) = electrostatic potential at point r
U = electric potential energy at point
r = test charge
Ke = Coulomb constant
Conservation of energy
When we talk about interactions between electric charges, conservation of energy tells us something fundamental that is explained below. The total energy remains constant unless external forces or dissipations intervene. We can practically say that with regards to the interaction between electric charges, conservation of energy is completely similar to what happens in the conservation of mechanical energy.
In fact, in the principle of conservation of mechanical energy it tells us that the total mechanical energy is equal to the kinetic energy plus the potential energy which in turn is constant
Relationship between field and potential and equipotential surfaces
For this topic we can say the following. The electrostatic potential is linked to the electric field through an integration operation. From this relationship we know how through knowledge at each point of the potential we can calculate the electric field locally.
When we relate electric fields, potentials and equipotential surfaces we can say the following:
Electric potential = energy at a point
Electric field = direction in which a charge slides
Equipotential surfaces = areas with the same level
Stokes' Theorem
Stokes' Theorem can be quite complicated, but it is a theorem that has important applications in fluid dynamics, electromagnetism and continuum mechanics.
This theorem, in simple terms, says that the movement or rotation of a vector field inside a surface can be described only by looking at what happens along the edge of that surface.
Poisson's Equation
We talked about Maxwell's equations before, these are related to the properties of the electrostatic field. If we express the field as a function of the potential and replace the first Maxwell equation we obtain the reference equation for the electrostatics associated with the potential. We will therefore obtain a differential equation that is called Poisson's equation.
Below is the mathematical form of the Poisson equation:
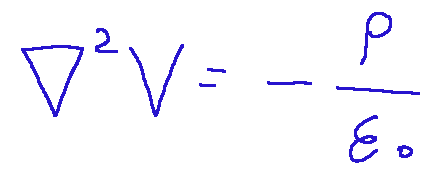
Where:
∇^2𝑉 = Laplacian of the potential, i.e. a measure of how much the potential changes in space
ρ = the density of electric charge
ε0 = the permittivity constant of the vacuum
Conclusions
Electric charges interact with each other generating forces of attraction or repulsion, described by Coulomb's law. These interactions occur through the electric field, an invisible force that each charge generates around itself, exactly like the force of gravity.
Question
Maxwell was a brilliant scientist who completely described electromagnetism with his equations, but did you also know that he was the one who made the first color photography experiment?

ITALIAN

25-04-2025 - Fisica - Interazioni tra cariche elettriche e potenziale [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_48-47-46-45)
Interazioni tra cariche elettriche e potenziale

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Il moto delle cariche elettriche
Prima di tutto definiamo un concetto che è quello delle linee di forza di un campo elettrico ora.
Queste sono rappresentazioni grafiche che mostrano la direzione e l’intensità del campo elettrico in una regione dello spazio. Le caratteristiche delle linee di forza di un campo elettrico sono elencate qui sotto:
Direzione
Intensità
Regola della tangente
Linee chiuse o aperte
Ora definiamo meglio l’importanza del moto delle cariche elettriche. Che cos’è il moto delle cariche elettriche? Possiamo dire che questo è il cuore di tutto ciò che ha a che fare con la corrente elettrica. Quello che viene definito moto delle cariche elettriche in fisica è semplicemente lo spostamento delle cariche elettriche all’interno di un materiale. Quando parliamo di moto di cariche elettriche, semplicemente e sostanzialmente stiamo parlando della famosissima corrente elettrica.
Il moto del dipolo
Senza addentrarci troppo all’interno del concetto di moto del dipolo elettrico, semplicemente scrivo che esso si riferisce al movimento di un dipolo elettrico (descritto nel post precedente) sotto l’azione di un campo elettrico esterno. Perché è importante questo concetto? Perché in un sistema del genere il dipolo elettrico può essere soggetto a traslazione. Cioè, se il dipolo è immerso in un campo elettrico uniforme, subirà una forza netta che può farlo muovere linearmente nello spazio.
Il teorema di Gauss
Il teorema di gauss è uno dei teoremi principali dei campi elettrici e quando parliamo di questo teorema è bene sapere che cos’è il flusso del campo elettrico. Questo è una misura della quantità di campo elettrico che attraversa una superficie. Viene considerata una grandezza fondamentale nell’elettromagnetismo. La legge di gauss ed una delle equazioni di Maxwell descrivono meglio il flusso del campo elettrico.
Definizione tecnica
Il teorema di Gauss afferma che il flusso del campo elettrostatico nel vuoto E0, attraverso una superficie chiusa qualunque S è pari alla somma algebrica (ovvero all’integrale nel caso di distribuzione continua) delle cariche contenute all’interno di S, diviso ε0.
Definizione semplificata
Il teorema di gauss, in parole semplici, possiamo dire che afferma che la quantità di campo elettrico che esce da una superficie chiusa dipende solo da quanta carica c’è dentro.
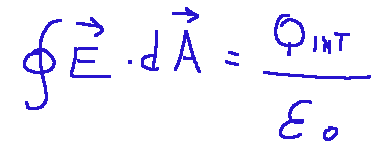
formula del teorema di Gauss
∮𝐸⋅𝑑𝐴 = flusso del campo elettrico attraverso una superficie chiusa
Q int = carica totale dentro la superficie
ε0 = costante chiamata permittività del vuoto
La prima equazione di Maxwell
Il teorema di Gauss e la prima equazione di Maxwell sostanzialmente sono la stessa cosa. Possiamo dire che il teorema di Gauss nasce come principio dell’elettrostatica mentre la prima equazione di Max generalizza questo teorema e lo inserisce in un contesto molto più ampio che è quello del sistema delle equazioni di Maxwell. Quest’ultime descrivono tutto l’elettromagnetismo.
Le distribuzioni uniformi
All’interno dell’argomento campi elettrici, quando parliamo di distribuzioni uniformi, andiamo a definire una cosa ben precisa. Che cos’è una distribuzione uniforme? Essa avviene quando una certa grandezza fisica è distribuita in modo costante lungo una lunghezza, superficie o volume. Quindi se parliamo di cariche elettrica, una distribuzione uniforme specifica che questa carica elettrica è distribuita in modo regolare sull’oggetto che stiamo studiando.
La distribuzione uniforme può essere anche sferica.
Potenziale elettrostatico
Il potenziale elettrico ed il potenziale elettrostatico più o meno sono la stessa cosa. Parliamo di potenziale elettrostatico quando siamo nel caso dell’elettrostatica, cioè con cariche ferme e campi elettrici statici. Ricordiamo che un campo elettrico statico è semplicemente un campo elettrico che non cambia nel tempo.
La formula del Potenziale elettrostatico è la seguente:
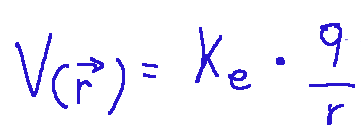
Dove:
V( r) = potenziale elettrostatico nel punto r
U = energia potenziale elettrica nel punto
r = carica di prova
Ke = costante di Coulomb
Conservazione dell’energia
Quando parliamo di interazioni tra cariche elettriche, la conservazione dell’energia ci dice una cosa fondamentale che è quella spiegata qui di seguito. L’energia totale rimane costante a meno che non intervengano forze esterne o dissipazioni. Praticamente possiamo dire che per quanto riguarda l’interazione tra cariche elettriche, la conservazione dell’energia, è del tutto simile a quello che succede nella conservazione dell’energia meccanica.
Infatti, nel principio di conservazione dell’energia meccanica ci dice proprio che l’energia meccanica totale è uguale all’energia cinetica più l’energia potenziale che a sua volta è costante
Relazione tra campo e potenziale e superfici equipotenziali
Per questo argomento possiamo dire quanto segue. Il potenziale elettrostatico è legato al campo elettrico mediante un’operazione di integrazione. Da questa relazione sappiamo come attraverso la conoscenza in ogni punto del potenziale si possa calcolare il campo elettrico localmente.
Quando mettiamo in relazione campo elettrici, potenziali e superfici equipotenziali possiamo dire quanto segue:
Potenziale elettrico = energia in un punto
Campo elettrico = direzione in cui scivola una carica
Superfici equipotenziali = zone con lo stesso livello
Teorema di Stokes
Il teorema di Stokes può risultare abbastanza complicato, ma è un teorema che ha applicazioni importanti in fluidodinamica, in elettromagnetismo e nella meccanica dei continui.
Questo teorema, in parole semplici, dice che il movimento o la rotazione di un campo vettoriale dentro una superficie può essere descritto solo guardando cosa succede lungo il bordo di quella superficie.
Equazione di Poisson
Prima abbiamo parlato delle equazioni di Maxwell, queste sono relative alle proprietà del campo elettrostatico. Se si esprime il campo in funzione del potenziale e si sostituisce alla prima equazione di Maxwell si ottiene invece l’equazione di riferimento per l’elettrostatica associata al potenziale. Otterremo quindi un’equazione differenziale che prende appunto il nome di equazione di Poisson.
Qui di seguito la forma matematica dell’equazione di Poisson:
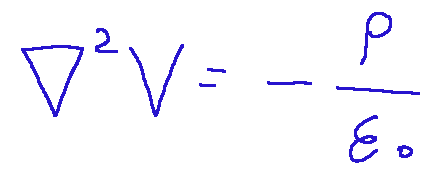
Dove:
∇^2𝑉 = Laplaciano del potenziale, cioè una misura di quanto cambia il potenziale nello spazio
ρ = la densità di carica elettrica
ε0 = la costante di permittività del vuoto
Conclusioni
Le cariche elettriche interagiscono tra loro generando forze di attrazione o repulsione, descritte dalla legge di Coulomb. Queste interazioni avvengono tramite il campo elettrico, una forza invisibile che ogni carica genera intorno a sé, esattamente come fa la forza di gravità.
Domanda
Maxwell fu uno scienziato geniale che con le sue equazioni descrisse l'elettromagnetismo in maniera completa, ma sapevate anche che fu lui a fare il primo esperimento di fotografia a colori?
THE END