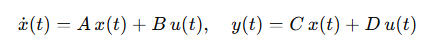~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

24-07-2025 - Systems Analysis - Building a Dynamic Model [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic mentioned above.
(code notes: X_76)

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
In systems analysis and modeling, a real-world case is taken and studied analytically. To simplify the concept as much as possible, systems analysis is a subject that teaches how to transform a real-world problem into a mathematical problem for the purpose of accurate analysis.
Systems analysis is an analytical approach that breaks down a system into processes, flows, and functions.
Real systems then become mathematical models. The most discussed mathematical models in Systems Analysis and Modeling are dynamic models, i.e., mathematical models with differential equations used, for example, in structural simulation.
Dynamic System
Before creating a dynamic system, it is useful to know what a dynamic system actually is. By definition, it is a mathematical model that describes the evolution over time of one or more internal states of a given system. The evolution of the dynamic model is what occurs in response to initial conditions and external inputs.
Note: When a dynamic model is formulated as a differential equation in the input variable u(t) and the output variable y(t) and their higher-order derivatives, alternative formulations are not possible.
A concrete example is the RLC circuit, i.e., a circuit in which a resistor, an inductor, and a capacitor are connected in series.
Below is an image of an RLC circuit.
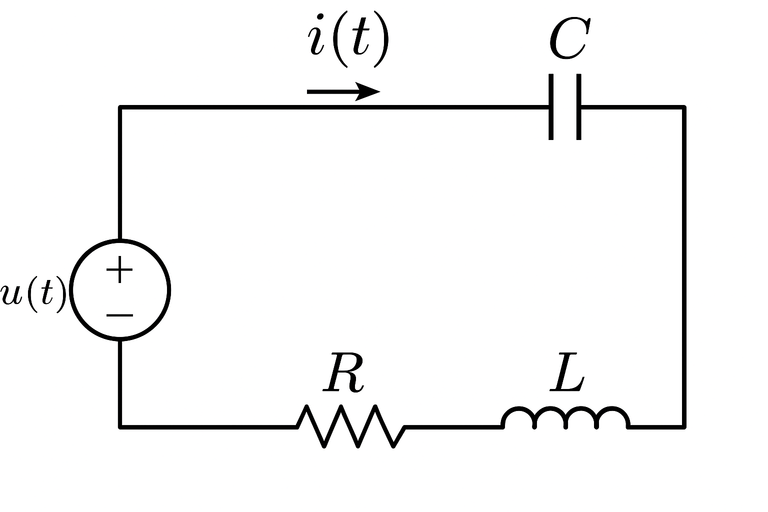
image created with artificial intelligence, the software used is ChatGPT
A series RLC circuit is a classic example of a linear time-invariant (LTI) dynamical system. It is a physical system that evolves over time, and its output depends on the input, its initial conditions, and even past conditions. However, the RLC circuit represents a case in which the input-output description is complete and closed. This case, as I wrote in the note above, leaves no room for alternative formulations.
Transformations of Dynamical Systems
Dynamic systems undergo transformation, and the main transformation is the transition from the transfer function to the state variables and vice versa.
Understanding the transfer function is not easy, especially if you are new to the subject and have never taken a course in Systems Analysis and Modeling. The transfer function is an algebraic representation of the behavior of a linear time-invariant (LTI) system in the Laplace domain.
This definition is probably already very complicated and difficult to understand.
Now let's look at the transfer function and a state-variable model, to better understand that it is possible to transition from the transfer function to the state variables and vice versa.
Transfer function
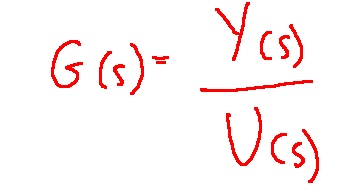
State variables
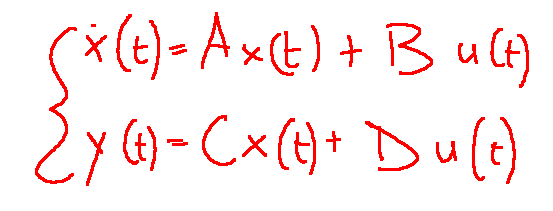
Transfer function to state variables
To perform this transfer, follow the steps described below:
-Start with the transfer function G(s)
-Transform everything into a differential equation
-Identify a set of state variables
-Obtain the model in canonical form
Why is the transition from transfer functions to state variables made in systems analysis?
This type of transformation allows the system analyst to understand the internal dynamics of the system and design the control module appropriately. Those working in the automation sector are able to make the transition in both directions, and feedback systems can also be designed in this way.
Below is a diagram explaining the transition from transfer function to state variables.
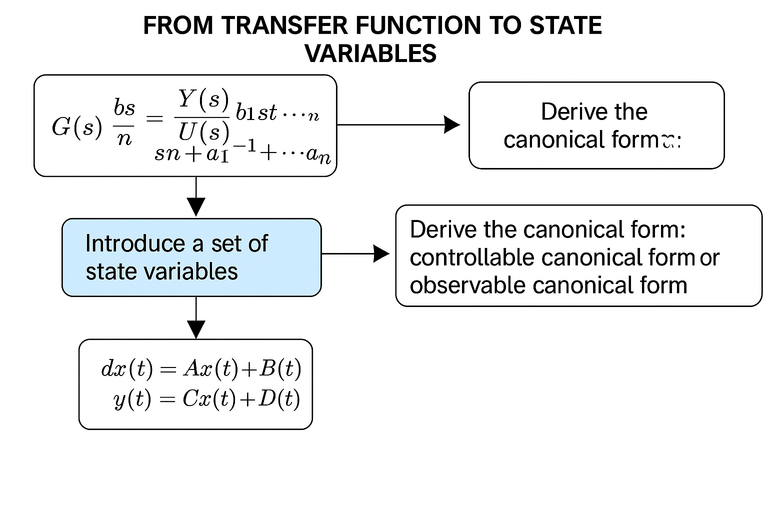
Image created with artificial intelligence, the software used is ChatGPT
Conclusions
At the end of all this, the question arises: why do we need to build a dynamic model of a real system? The answer to this question is much simpler than the entire explanation I've attempted in this article. We need to build a dynamic model of a real system because only in this way can we mathematically represent the behavior of that system over time and predict its evolution.
For example, imagine a ball rolling along a path. The ball's velocity and position change over time, depending on friction and the force applied. The static model would only provide us with information about where the ball will be at a given moment, while the dynamic model helps us visualize the entire path the ball will take and predict where it will end up. The dynamic model explains the evolution of a system.
Question
Did you know that one of the most famous dynamic models is the three-body problem studied by Henri Poincaré in the 19th century? Did you know that the French mathematician and physicist described the motion of three celestial bodies, which gravitationally attract each other, thus revolutionizing the understanding of complex dynamical systems because a small change in the initial conditions can lead to very different behaviors?

ITALIAN

24-07-2025 - Analisi dei sistemi - Realizzare un modello dinamico [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_76)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
In analisi e modellistica dei sistemi si prende un caso reale e lo si studia in maniera analitica. Semplificando il concetto il più possibili, l'analisi di sistemi è una materia che insegna come trasformare un problema reale in un problema matematico con lo scopo di fare analisi accurate.
L'analisi dei sistemi è un approccio analitico che scompone un sistema in processi, flussi e funzioni.
Quindi i sistemi reali diventano modelli matematici. I modelli matematici più discussi nell'ambito dell'Analisi e modellistica di Sistemi sono i modelli dinamici, ovvero i modelli matematici con equazioni differenziali usare per esempio nella simulazione strutturale.
Sistema dinamico
Prima di realizzare un sistema dinamico, sarà utile sapere cosa sia in realtà un sistema dinamico. Per definizione esso è un modello matematico che descrive l'evoluzione nel tempo di uno o più stati interni di un determinato sistema. L'evoluzione del modello dinamico è ciò che avviene in risposta alle condizioni iniziali e agli ingressi esterni
Nota: Quando un modello dinamico è formulato come equazione differenziale nella variabile di ingresso u(t) e nella variabile di uscita y(t) e delle relative derivate di ordine superiore, non sono possibili formulazioni alternative.
Un esempio concreto può essere il circuito RLC, cioè un circuito in cui sono collegate in serie una resistenza, un'induttanza e un condensatore.
Qui di seguito un'immagine di un circuito RLC

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Un circuito RLC in serie è un classico esempio di sistema dinamico lineare tempo-invariante (LTI). Esso è un sistema fisico che si evolve nel tempo e la sua uscita dipende dall'ingresso, dalle sue condizioni iniziali e anche da quelle del passato, però il circuito RLC rappresenta un caso in cui la descrizione input-output è completa e chiusa. Questo caso, come ho scritto nella nota qui sopra, non lascia spazio a formulazioni alternative.
Le trasformazioni dei sistemi dinamici
I sistemi dinamici si trasformano e la trasformazione principale è il passaggio dalla funzione di trasferimento alle variabili di stato e viceversa.
Comprendere la funzione di trasferimento non è facile, soprattutto se si è nuovi e non si è mai fatto un corso di Analisi e Modellistica dei sistemi. La funzione di trasferimento è una rappresentazione algebrica del comportamento di un sistema lineare tempo-invariante (LTI) nel dominio di Laplace.
Questa definizione probabilmente è già di per sé molto complicata e di difficile comprensione.
Ora vediamo come si presentano la funzione di trasferimento e un modello a variabili di stato, per meglio comprendere che si può passare dalla funzione di trasferimento alle variabili di stato e viceversa.
funzione di trasferimento
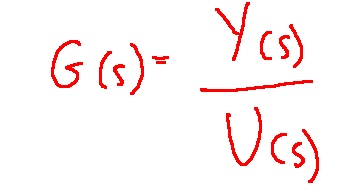
variabili di stato
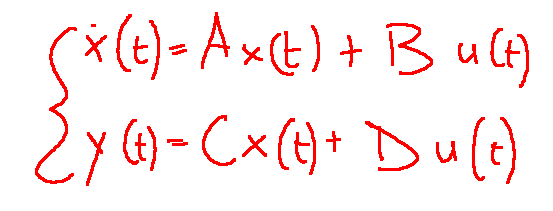
Passaggio da funzione di trasferimento a variabili di stato
Per effettuare questo trasferimento bisogna osservare i seguenti passaggi descritti qui sotto:
-Si parte dalla funzione di trasferimento G(s)
-Si trasforma il tutto in un equazione differenziale
-Si individua un insieme di variabili di stato
-Si ricava il modello in forma canonica
Perché in analisi dei sistemi si effettua il passaggio da funzione di trasferimento a variabili di stato?
Questa sorta di trasformazione permette a chi sta analizzando il sistema di comprendere la dinamica interna del sistema e progettare i modulo di controllo in maniera adeguata. Chi lavora nel settore dell'automazione è in grado di effettuare il passaggio in entrambe le direzioni ed in questa maniera si possono progettare anche sistemi a retroazione.
Qui di seguito uno schema dove è spiegato il passaggio da funzione di trasferimento a variabili di stato
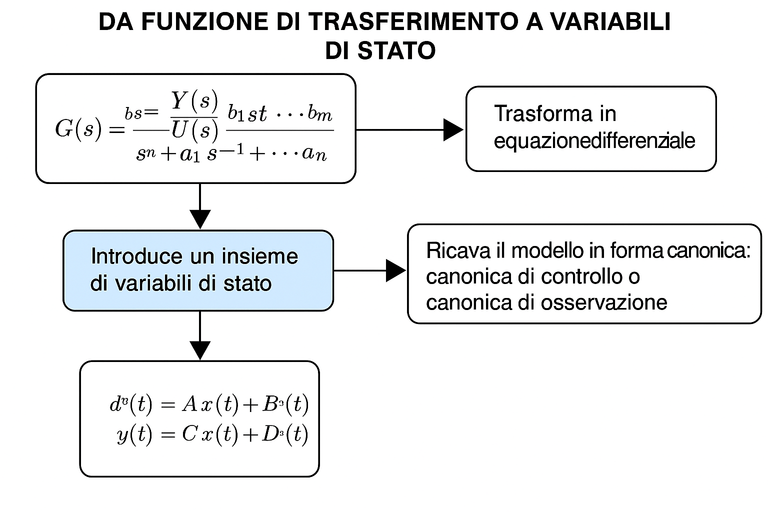
immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Conclusioni
Alla fine di tutto questo ci si chiede, perché dobbiamo realizzare un modello dinamico di un sistema reale? La risposta a questa domanda è molto più semplice di tutta la spiegazione che ho provato a fare in questo articolo. Dobbiamo realizzare un modello dinamico di un sistema reale perché solo così possiamo rappresentare matematicamente il comportamento di quel sistema nel tempo e prevederne l'evoluzione.
Facciamo un esempio, pensiamo di avere un percorso su cui rotola una pallina. La velocità e la posizione della pallina cambia nel tempo, cambia in base all'attrito e alla forza impressa. Il modello statico ci darebbe solo l'informazione di dove si troverà la pallina in un determinato istante, mentre invece il modello dinamico ci aiuta a vedere tutta la corsa che farà la pallina e a prevedere dove finirà. Il modello dinamico spiega l'evoluzione di un sistema.
Domanda
Lo sapevate che uno dei modelli dinamici più famosi è quello del problema dei tre corpi studiato da Henri Poincaré nel XIX secolo? Lo sapevate che il matematico e fisico francese descrisse il moto di tre corpi celesti, che si attraggono gravitazionalmente rivoluzionando così la comprensione dei sistemi dinamici complessi in quanto una piccola variazione? Lo sapevate che il suo modello dinamico dimostrò che piccole variazioni nelle condizioni iniziali possono portare a comportamenti molto diversi?
THE END