
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

20-06-2025 - Systems Analysis - Analytical Model [EN]-[IT]
With this post I would like to give a brief instruction regarding the topic mentioned in the subject
(code notes: X_86)
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
The study of systems is important to set up a project, a process or a control device within a production chain.
Analytical model of the elements of a system
Here we are to talk about the key point of systems analysis and modeling.
The main concept of this discipline is to represent systems mathematically in order to improve processes and have an efficient feedback loop. However, we must consider that most likely we are thinking of a system that is to be applied in an industrial context and therefore we are thinking of a real system. But if we have to do calculations and measure the efficiency of a system we need a mathematical model. And here comes the analytical model to help.
The analytical model is the tool that allows us to transform a real system into a mathematical system. This transformation will allow us to study the system in a rigorous way.
Description of dynamic behavior
image created with artificial intelligence, the software used is napkin.ai
The dynamic behavior of a system can be described by an analytical relation in which appear:
-The instantaneous values of the output variables
-The instantaneous values of the input variables
-The instantaneous values of the derivative of the dynamic behavior
Below is shown the function of the instantaneous values of the output variables y(t) and of the input variables u(t)
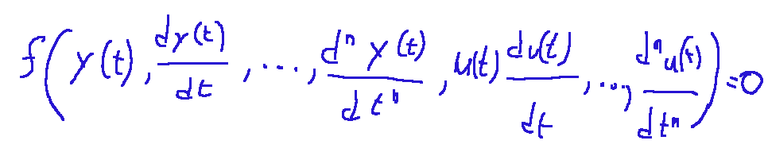
This just described is a mathematical relationship typical of dynamic systems modeling and here we return to the main topic of this article on systems analysis.
The dynamic behavior of many elements, which make up a system, can be described by an analytical relationship where y(t) are the instantaneous values of the output variables, while u(t) are the instantaneous values of the input variables.
Be careful because the mathematical relationship also includes the derivatives of both up to a certain order n for the output and m for the input.
The image below specifies the terms of the derivatives just described

What does that mathematical relationship mean?
It means that the system is described by a function f that cancels this combination of inputs, outputs and their derivatives.
Use of the Analytical Model
The mathematical relationship shown before, even if it seems complex, can actually be considered among the simplest in the context of analytical models of a dynamic system. This mathematical relationship can be used in many fields and can represent:
-physical systems
-mechanical systems
-electrical systems
-chemical systems
Some information about analytical models
First of all we need to clarify the concept of "initial conditions of a system", what are they?
The initial conditions of a system is simply the initial state of the system, from then on the system will be subject to changes.
A linearized model is a linear model approximating the nonlinear model of a system
What is very important is to understand that the mathematical model that is generally given of dynamic systems is the differential equation.
The state space model of a system
How is the state space model of a system structured?
It consists of two equations: the state evolution equation and the output equation. The state equation expresses the evolution of the state as a function of the present state and the input. The output equation expresses the output as a function of the state and the input.
Here is an example of an equation of state
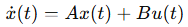
Here is an example of an output equation
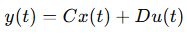
Conventional Letters
In system analysis and modeling, the following letters are used to identify analytical models:
x → state of the system
u → input
y → output
z → rarely used for state, may indicate other auxiliary variables
Conclusions
In system analysis and modeling, real systems are transformed into mathematical models, the analytical model is the model that transforms a real system into a mathematical model. Furthermore, the analytical model also has its own logical importance, it allows you to see how each part of the system contributes to its overall behavior,
Question
The analytical model is the physically founded starting point to represent a dynamic system starting from its elementary structure. Did you know that in the analytical model, differential equations are extremely important and that Isaac Newton is considered a pioneer of the analytical model?

ITALIAN

20-06-2025 - Analisi dei sistemi - Modello analitico [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_86)

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Lo studio dei sistemi è importante per imbastire un progetto, un processo o un apparato di controllo all'interno di una catena di produzione.
Modello analitico degli elementi di un sistema
Eccoci qua a parlare del punto chiave dell’analisi e modellistica dei sistemi.
Il concetto principale di questa disciplina è quello di rappresentare i sistemi matematicamente in maniera da migliorare i processi ed avere un ciclo di feedback efficiente. Dobbiamo però considerare che molto probabilmente noi stiamo pensando ad un sistema che è da applicare in un contesto industriale e quindi stiamo pensado ad un sistema reale. Ma se dobbiamo fare conti e misurare l’efficienza di un sistema abbiamo bisogno di un modello matematico. Ed ecco che arriva in aiuto il modello analitico.
Il modello analitico è lo strumento che permette di trasformare un sistema reale in un sistema matematico. Questa trasformazione ci permetterà di studiare il sistema in modo rigoroso.
Descrizione del comportamento dinamico

immagine creata con l’intelligenza artificiale, il software usato è napkin.ai
Il comportamento dinamico di un sistema può essere descritto da una relazione analitica in cui compaiono:
-I valori istantanei delle variabili di uscita
-I valori istantanei delle variabili in ingresso
-I valori istantanei della derivata del comportamento dinamico
Qui di seguito è mostrata la funzione dei valori istantanei delle variabili d'uscita y(t) e delle variabili di ingresso u(t)
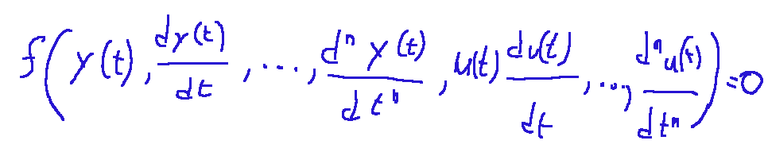
Questa appena descritta è una relazione matematica tipica della modellistica dei sistemi dinamici e qui ci riconduciamo all'argomento principale di questo articolo sull'analisi dei sistemi.
Il comportamento dinamico di molti elementi, che costituiscono un sistema, può essere descritto da una relazione analitica dove y(t) sono i valori istantanei delle variabili d'uscita, mentre u(t) sono i valori istantanei delle variabili di ingresso.
Attenzione perché nella relazione matematica compaiono anche le derivate di entrambi fino a un certo ordine n per l’uscita e m per l’ingresso.
Nell'immagine qui sotto sono specificate i termini delle derivate appena descritte

Cosa significa quella relazione matematica?
Significa che il sistema è descritto da una funzione f che annulla questa combinazione di ingressi, uscite e le loro derivate.
Uso del Modello analitico
La relazione matematica mostrata prima, anche se sembra complessa, in realtà si può considerare tra le più semplici nell'ambito dei modelli analitici di un sistema dinamico. Questa relazione matematica però può essere usata in molti ambiti e può rappresentare:
-sistemi fisici
-sistemi meccanici
-sistemi elettrici
-sistemi chimici
Alcune informazioni a riguardo dei modelli analitici
Innanzitutto dobbiamo chiarire il concetto di "condizioni iniziali di un sistema", cosa sono?
Le condizioni iniziali di un sistema è semplicemente lo stato iniziale del sistema, da li in poi il sistema sarà soggetto a cambiamenti.
Un modello linearizzato è un modello lineare approssimante il modello non lineare di un sistema
Cosa invece molto importante è capire che il modello matematico che si da in genere dei sistemi dinamici è l'equazione differenziale.
Il modello nello spazio di stato di un sistema
Come è strutturato il modello nello spazio di stato di un sistema?
Consiste di due equazioni: l'equazione dell'evoluzione dello stato e l'equazione dell'uscita. L'equazione dello stato esprime l'evoluzione dello stato in funzione dello stato presente e dell'ingresso. L'equazione dell'uscita esprime l'uscita in funzione dello stato e dell'ingresso.
Qui di seguito un esempio di un equazione di stato
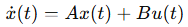
Qui di seguito un esempio di un equazione di uscita
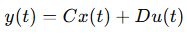
Lettere convenzionali
Nell'analisi e modellistica di sistemi per identificare i modelli analitici si usano le seguenti lettere:
x → stato del sistema
u → ingresso (input)
y → uscita (output)
z → raramente usata per lo stato, può indicare altre variabili ausiliarie
Conclusioni
In analisi e modellistica dei sistemi si trasformano i sistemi reali in modelli matematici, il modello analitico è quel modello che trasformare un sistema reale in un modello matematico. Inoltre il modello analitico ha anche una sua importanza logica, permette di vedere come ogni parte del sistema contribuisce al suo comportamento complessivo,
Domanda
Il modello analitico è il punto di partenza fisicamente fondato per rappresentare un sistema dinamico a partire dalla sua struttura elementare. Lo sapevate che nel modello analitico le equazioni differenziali sono di estrema importanza e che si considera Isaac Newton un pioniere del modello analitico?
THE END