
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
19-11-2024 - Analytical Geometry - Gauss-Jordan Elimination Method [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_74)
Gauss-Jordan Elimination Method
Description
To calculate the solutions of a compatible system of linear equations, the Gauss-Jordan elimination method can also be used.
Example
Let's try to find the set of solutions of the following system of real linear equations with the Gauss-Jordan elimination method.
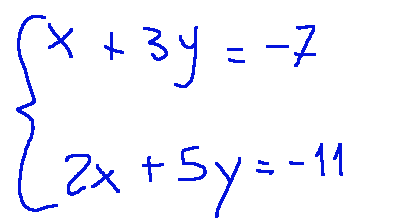
Given this system of linear equations, let's write it in augmented matrix form (known coefficients and terms)
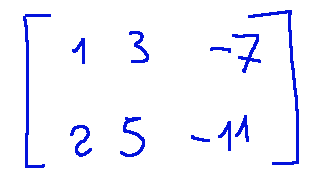
-1 Initial step
Let's normalize the first row. As soon as we start to do this we can see that the first row is already normalized (the first element is 1)
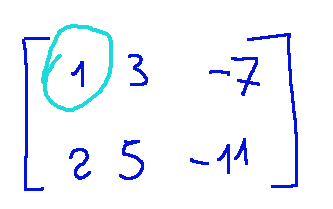
-2 Step 2
Remove the coefficient in the second row
To do this we subtract the first row from the second row 2 times, that is…
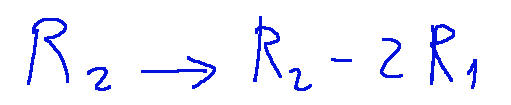
We will have that the matrix will transform as follows:
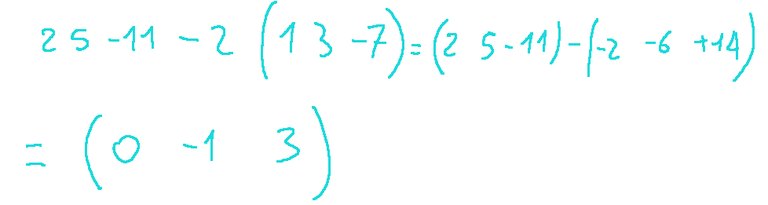
Here is the processed matrix.
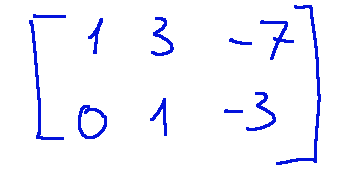
-3 Third step
In this step we normalize the second row
To do this we divide the second row by -1 to get a coefficient of 1 in position a22
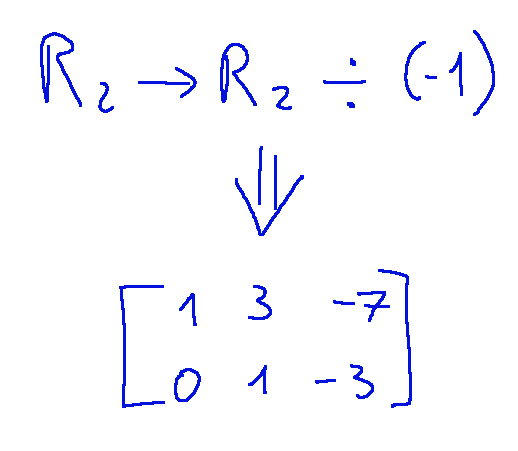
-4 Fourth step elimination
In this step we can eliminate the coefficient in the first row.
To do this, that is, to eliminate the coefficient 3 in the first row, we subtract 3 times the second row.
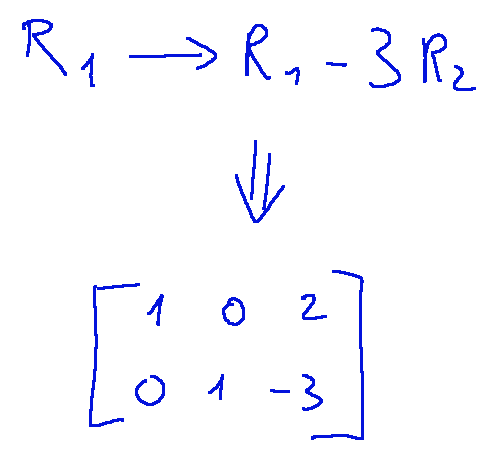
So now we have arrived towards the end of the procedure.
The reduced matrix is
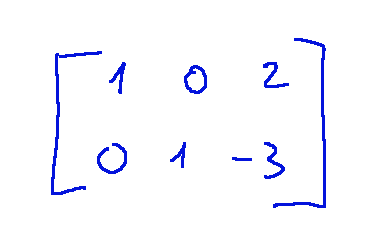
which corresponds to the system…
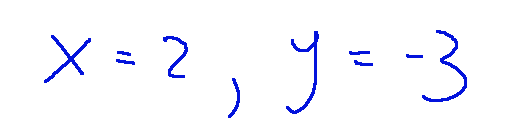
Result
x = 2, y = -3
Conclusions
We can state the following. The Gauss-Jordan elimination method is a systematic procedure for solving systems of linear equations by transforming an augmented matrix into a scale-reduced form (row by row)
Question
Did you study the Gauss-Jordan elimination method in school?

[ITALIAN]
19-11-2024 - Geometria analitica - Metodo di eliminazione di Gauss-Jordan [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_74)
Metodo di eliminazione di Gauss-Jordan
Descrizione
Per calcolare le soluzioni di un sistema di equazioni lineari compatibile si può utilizzare anche il metodo di eliminazione di Gauss-Jordan.
Esempio
Proviamo a trovare l’insieme delle soluzioni del seguente sistema di equazioni lineare reali con il metodo di eliminazione di Gauss-Jordan.
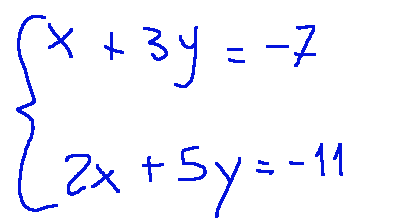
Dato questo sistema di equazioni lineari passiamo a scriverlo in forma di matrice aumentata (coefficienti e termini noti)
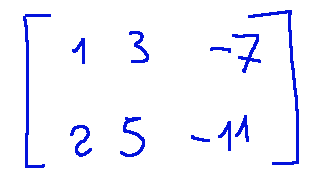
-1 Passo iniziale
Normalizziamo la prima riga. Appena ci accingiamo a fare questa operazione possiamo notare che la prima riga è già normalizzata (il primo elemento è 1)
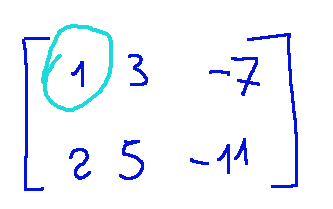
-2 Passo 2
Eliminare il coefficiente nella seconda riga
Per fare questo sottraiamo 2 volte la prima riga dalla seconda riga, cioè…
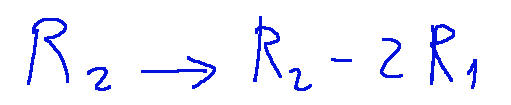
Avremo che la matrice si trasformerà come segue:
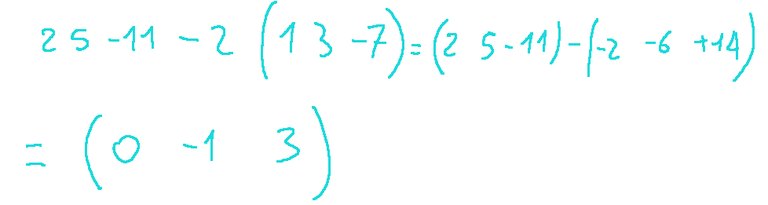
Ecco la matrice elaborata.
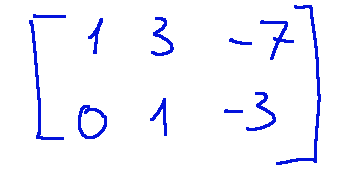
-3 Passo terzo
In questo passaggio normalizziamo la seconda riga
Per fare questo dividiamo la seconda riga per -1 per ottenere un coefficiente 1 nella posizione a22
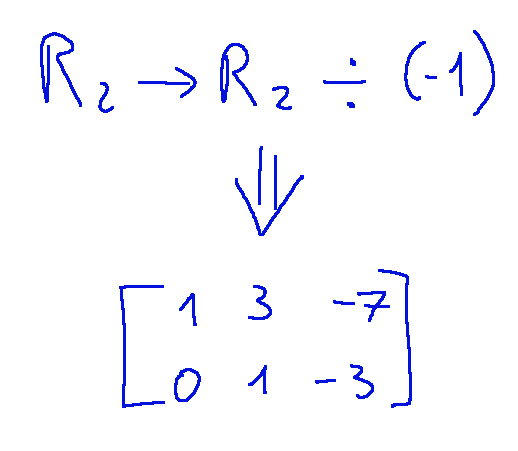
-4 Passo quarto eliminazione
In questa fase possiamo eliminare il coefficiente nella prima riga.
Per fare questo, cioè per eliminare il coefficiente 3 nella prima riga, sottraiamo 3 volte la seconda riga.

Quindi ora siamo arrivate verso la fine del procedimento.
La matrice ridotta è
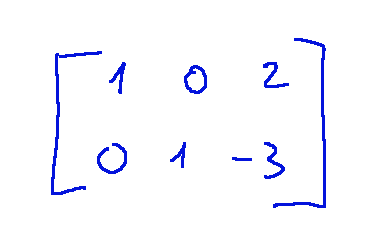
che corrisponde al sistema…
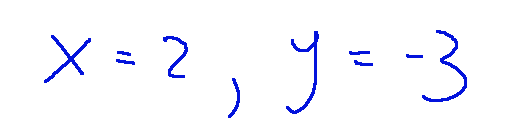
Risultato
x = 2, y = -3
Conclusioni
Possiamo affermare quanto segue. Il metodo di eliminazione di Gauss-Jordan è una procedura sistematica per risolvere sistemi di equazioni lineari trasformando una matrice aumentata in forma ridotta a scala (riga per riga)
Domanda
Avete studiato a scuola il metodo di eliminazione di Gauss-Jordan?
THE END
