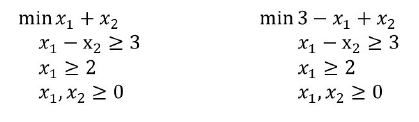~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

18-06-2025 - Operations Research - Linear Programming [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_93)
Linear Programming
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Operations research is fundamentally based on linear programming.
Basically, linear programming is a mathematical approach to solving optimization problems.
What does solving optimization problems mean?
It means finding the best solution among all the possible solutions respecting a criterion and the constraints.
Optimization is equivalent to choosing the optimal values of some variables to maximize or minimize a function.
Elements of a problem
image created with artificial intelligence, the software used is Napkin.ai
When we face a linear programming problem we will have some elements of optimization. These elements are listed below.
-Decision variables
-Objective function
-Constraints
Below is written a linear programming problem in general form.
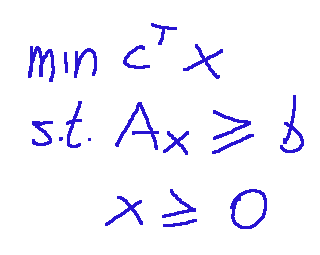
Example 01
Let's take the following linear programming problem as an example
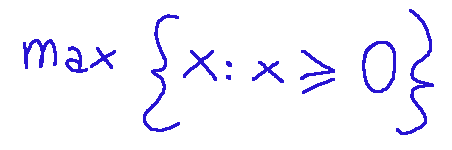
So we want to maximize x such that x is greater than or equal to ZERO.
We can also read this mathematical description as wanting to determine the maximum value of x among all real numbers greater than or equal to zero.
In particular, this ...

...represents the set of all values of x such that x is greater than or equal to zero.
The goal
In this linear programming problem, we want to find the largest possible value of x while respecting the condition that x cannot be negative.
Going to analyze the admissible set we see that it is the following:
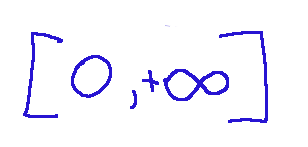
As for the objective function in this case we are in a simple case since it is x.
We can now arrive at a logical deduction, which is the one that is trying to maximize x without an upper bound.
So we can say that in this linear programming problem x is arbitrarily large, there is no finite maximum, it does not admit an optimal solution, the feasible set is not empty as it includes all values >= 0
Solution
This linear programming problem is unbounded above
Example 02
Let's now take another particular problem.

This problem asks to minimize the minimum value of the function 2x among all the values of (x,y) that simultaneously satisfy the constraints:
x+y=1
x+y<=0
{2x :...}, this indicates that we are trying to minimize the objective function 2x.
Now we report the constraints below:
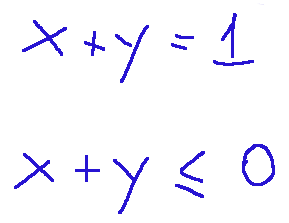
We can immediately deduce that there cannot be a pair (x,y) that satisfies both the given constraints, at this point we deduce that the feasible set is empty!
Result
This linear programming problem has no solution.
Conclusions
Linear programming is used to find the decision variables that maximize or minimize an objective function respecting given constraints. Tackling a problem by studying it with linear programming could help to make optimal decisions. Linear programming can be used to make optimal decisions in for example planning, manufacturing of a product or in a logistics problem.
Question
Did you know in 1955 Exxon / Shell engineers brought linear programming into the various companies and optimized refineries, chemical plants, logistics and corporate budgeting?

ITALIAN

18-06-2025 - Ricerca operativa - La programmazione lineare [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_93)
La programmazione lineare
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
La ricerca operativa si base fondamentalmente sulla programmazione lineare.
Sostanzialmente la programmazione lineare è un approccio matematico per risolvere problemi di ottimizzazione.
Cosa vuol dire risolvere problemi di ottimizzazione?
Significa trovare la soluzione migliore tra tutta le soluzioni possibili rispettando un criterio e i vincoli.
Ottimizzare equivale a scegliere i valori ottimali di alcune variabili per massimizzare o minimizzare una funzione.
Elementi di un problema

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
Quando affrontiamo un problema di programmazione lineare avremo degli elementi di ottimizzazione. Questi elementi sono elencati qui sotto.
-Variabili di decisione
-Funzione obiettivo
-Vincoli
Qui di seguito è scritto un problema di programmazione lineare in forma generale.
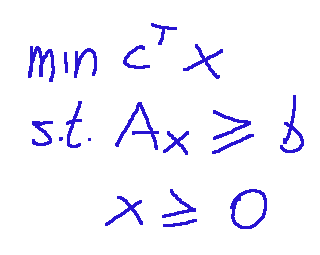
Esempio 01
Prendiamo come esempio il seguente problema di programmazione lineare
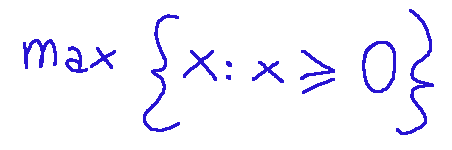
Quindi vogliamo massimizzare x tale che x sia maggiore o uguale a ZERO.
Possiamo anche leggere questa descrizione matematica come il fatto di voler determinare il massimo valore di x tra tutti i numeri reali maggiori o uguali a zero.
In particolare questo ...

...rappresenta l'insieme di tutti i valori di x tali che x è maggiore o uguale a zero.
L'obiettivo
In questo problema di programmazione lineare si vuole trovare il valore più grande possibile di x rispettando la condizione che x non può essere negativo.
Andando ad analizzare l'insieme ammissibile vediamo che è il seguente:
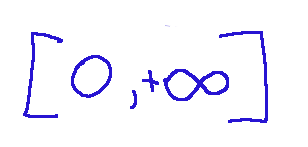
Per quanto riguarda la funzione obiettivo in questo caso rientriamo in un caso semplice in quanto è x.
Possiamo ora arrivare ad una deduzione logica, che è quella che so sta cercando di massimizzare x senza un limite superiore.
Quindi possiamo dire che in questo problema di programmazione lineare la x è arbitrariamente grande, non esiste un massimo finito, non ammette soluzione ottima, l'insieme ammissibile non è vuoto in quanto include tutti i valori >= 0
Soluzione
Questo problema di programmazione lineare è illimitato superiormente
Esempio 02
Prendiamo ora un altro problema particolare.

Questo problema chiede di minimizzare il valore minimo della funzione 2x tra tutti i valori di (x,y) che soddisfano contemporaneamente i vincoli:
x+y=1
x+y<=0
{2x :...}, questo indica che stiamo cercando di minimizzare la funzione obiettivo 2x.
Ora riportiamo qui sotto i vincoli:
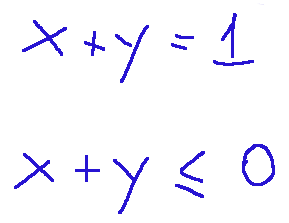
Possiamo subito dedurre che non può esistere una coppia (x,y) che soddisfi entrambi i vincoli dati, a questo punto deduciamo che l'insieme ammissibile è vuoto!
Risultato
Questo problema di programmazione lineare non ha soluzione.
Conclusioni
La programmazione lineare viene usata per trovare le variabili decisionali che massimizzano o minimizzano una funzione obiettivo rispettando dei vincoli dati. Affrontare un problema studiandolo con la programmazione lineare potrebbe aiutare a prendere delle decisioni ottimali. La programmazione lineare può essere usata per prendere decisioni ottimali in ad esempio nella pianificazione, nella produzione di un prodotto o in un problema di logistica.
Domanda
Lo sapevate nel 1955 gli ingegneri di Exxon / Shell portarono la programmazione lineare dentro le varie aziende ed ottimizzarono le raffinerie, gli impianti chimici, la logistica ed il budgeting aziendale?
THE END