~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

17-06-2025 - Operations Research - Definitions [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_97)
Definitions

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
In Operations Research we usually start by defining an optimization problem.
Here is an example:
Let's consider a non-empty set, that is:
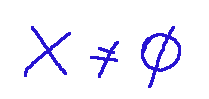
At this point we think that the following function is known:

This function makes sure that each element of the set X associates a real value in R.
Now let's explain what the minimization problem is
It is called the minimization problem

associated with the pair (X,f) the problem of determining the element...

of the set X in which the function f takes the minimum value.
This is mathematically expressed in the following way.
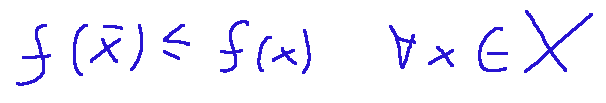
The element ...

... is called the minimum point of f in X
Example of an optimization problem
We take the definition set X of the variable x as the closed interval X = [1,3]. So:
-the domain of the function is X = [1,3]
-the objective function is f(x) = x^2
-the problem is: min {X^2 : 1 <= x <= 3}
let's consider the following function:
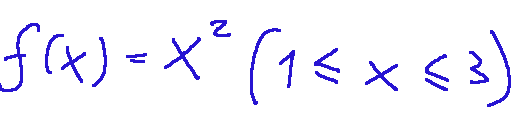
This writing means that we consider a function in x that is the square of x (x^2), but the values of x that we consider are only those between 1 and 3

Now consider the following optimization problem:
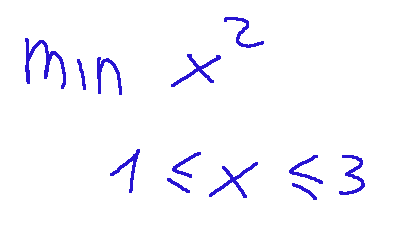
This is equivalent to saying, in the range of numbers from 1 to 3, what is the minimum value of x considering the function of x^2?
The optimum point, i.e. the value of the decision variable
x that achieves the minimum of the function in the given interval, is:

while the optimum value, i.e. the value that the function assumes at the optimum point is:
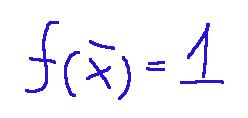
Some notes
Given the example just described we can say that:
Maximizing a real-valued function f on a set C is equivalent to Minimizing the function -f on the set C
A minimization optimization problem is unbounded below if, given a value M, there always exists a feasible solution with a value less than M
An optimization problem is unbounded either above or below. For example, the problem min{e-x: x ≥ 0} is unbounded below. Or a maximization optimization problem is unbounded above if given a value M there is always a feasible solution of value greater than M
Furthermore, it is good to remember that an optimization problem can:
or admit an optimal solution
or be infeasible
or be unbounded (below or above)
Conclusions
Operations Research is used to identify feasible solutions to a problem by defining the problem mathematically. The example proposed in this article is a simple optimization exercise. This example helps to see the practical logic behind Operations Research
Question
Operations Research is a fairly young school subject. Did you know that Operations Research began to be formally taught in universities only after 1960?

ITALIAN

17-06-2025 - Ricerca operativa - Definizioni [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_97)
Definizioni

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
In Ricerca Operativa solitamente si parte nel definire un problemi di ottimizzazione.
Qui di seguito un esempio:
Consideriamo un insieme non vuoto, ovvero:
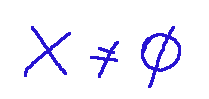
A questo punto pensiamo che sia nota la seguente funzione:

Questa funzione fa in modo che a ogni elemento dell'insieme X associ un valore reale in R.
Ora spieghiamo cosa è il problema di minimizzazione
Viene chiamato problema di minimizzazione

associato alla coppia (X,f) il problema di determinare l'elemento...

dell'insieme X in cui la funzione f assume il valore minimo.
Questo matematicamente si esprime nella seguente maniera.
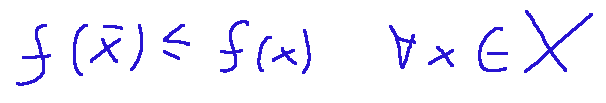
L'elemento ...

... viene detto punto di minimo di f in X
Esempio di problema di ottimizzazione
Prendiamo l'insieme di definizione X della variabile x come l'intervallo chiuso X = [1,3]. Quindi:
-il dominio della funzione è X = [1,3]
-la funzione obiettivo è f(x) = x^2
-il problema è: min {X^2 : 1 <= x <= 3}
consideriamo la seguente funzione:
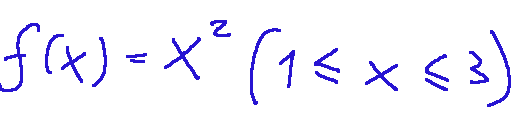
Questa scrittura significa che consideriamo una funzione in x che è il quadrato di x (x^2), ma i valori di x che consideriamo sono solo quelli compresi tra 1 e 3

Consideriamo ora il problema di ottimizzazione seguente:
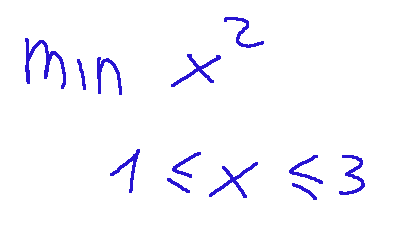
questo equivale a dire, nell'intervallo dei numeri che vanno da 1 a 3, qual è il valore minimo di x considerando la funzione di x^2?
Il punto di ottimo, cioè il valore della variabile di decisione
x che realizza il minimo della funzione nell’intervallo dato, è:

mentre il valore di ottimo, cioè il valore che la funzione assume nel punto di ottimo è:
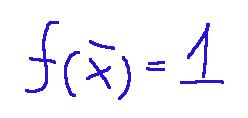
Alcune note
Visto l'esempio appena descritto possiamo dire che:
Massimizzare una funzione f a valori reali su un insieme C è equivalente a Minimizzare la funzione -f sull'insieme C
Un problema di ottimizzazione di minimizzazione è inferiormente illimitato se preso un valore M esiste sempre una soluzione ammissibile di valore minore di M
Un problema di ottimizzazione è illimitato o superiormente o inferiormente. Ad esempio Il problema min{e-x: x ≥ 0} è illimitato inferiormente. Oppure un problema di ottimizzazione di massimizzazione è superiormente illimitato se preso un valore M esiste sempre una soluzione ammissibile di valore maggiore di M
Inoltre è bene ricordare che un problema di ottimizzazione può:
o ammettere soluzione ottima
o essere inammissibile
o essere illimitato (inferiormente o superiormente)
Conclusioni
La Ricerca Operativa serve per identificare delle soluzioni ammissibili ad un problema definendo il problema in maniera matematica. L'esempio proposto in questo articolo è un semplice esercizio di ottimizzazione. Questo esempio aiuta a vedere la logica pratica che c'è dietro la Ricerca Operativa
Domanda
Ricerca Operativa è una materia scolastica abbastanza giovane. Lo sapevate che Ricerca Operativa iniziò ad essere formalmente insegnata nelle università solo dopo il 1960?
THE END
