
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

11-04-2025 - Physics - Momentum [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_79-78)
Momentum

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Momentum is defined and indicated with 𝒑, the product of the
mass (m) and the velocity (v) of a body according to the relationship shown here continuation:
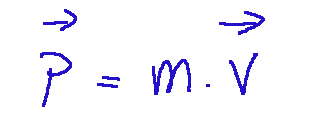
Where:
p = momentum
m = mass (expressed in kg)
v = velocity (expressed in m/s)
Momentum is a vector quantity that is particularly important when dealing with collisions between bodies and is such that it allows us to predict the magnitude, direction and direction of the velocity of the bodies after the collision. For example, the guard rail at the edge of a road must be able to slow down and stop the motion of a car that skids and goes off the road.
Unit of measure
The unit of measure of the quantity of motion in the International System (SI) is the kilogram meter per second.
We can also deduce this unit of measure by analyzing in two steps the formula of the quantity of motion expressed before.
first step
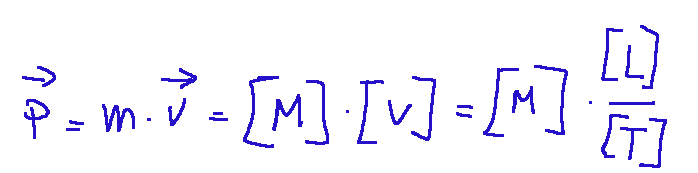
second step
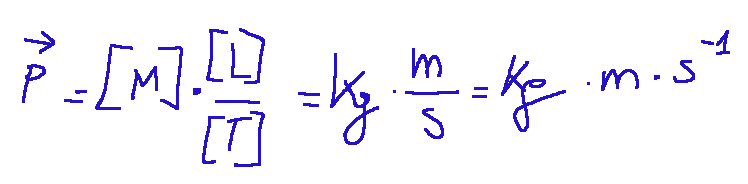
Conservation of momentum
What happens when two bodies collide?
Let's assume the case of two bodies of mass A and B that interact with each other considering a force for example attractive or repulsive (of an internal nature to the system we are considering, that is, deriving from the collision between the bodies).
The force that mass A exerts on mass B will be FAB while the force that mass B exerts on mass A will be FBA. By the third law of dynamics we know that the two forces will be equal in magnitude and direction but opposite in direction so that their vector sum is zero:

What does the principle of conservation of momentum say in a nutshell?
In an isolated system, the total momentum is conserved, that is, it remains constant over time, even if the individual bodies that compose it change speed or direction
Taking into account that two bodies A and B interact (for example in a collision), we know that the equation of the principle of conservation of momentum is the following:
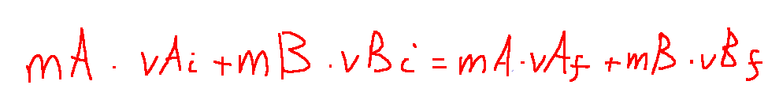
Written in this way, it seems like a rather complex formula, but in reality it is not, since it is enough to know that:
m = mass of the body
vi = initial velocity
vf = final velocity
From this formula we can deduce that the sum of the momentum before the collision is equal to the sum after.
As far as this topic is concerned, we can also give a more technical literal description that could be the following:
We can state that the principle of conservation of momentum: when the resultant of the external forces applied to a system is zero, that is, when the system is isolated, the momentum is conserved over time, that is, it always assumes the same value. Therefore, the variation of momentum in a certain time interval is always equal to 0.
NOTE: Generally, the momentum is calculated by considering the mass of the body as constant. However, the mass of a body can also vary. Therefore, in some physical problems I must consider it variable.
Momentum Scientists

image created with artificial intelligence, the software used is Microsoft Copilot
Momentum scientists are very well known in the field of scientific history. Here is a list of scientists who contributed to the study of momentum:
-Galileo Galilei (1564–1642)
-René Descartes (Cartesio)
-Isaac Newton
-Leonhard Euler
-Emmy Noether
Impulse of a force
The impulse of a force in physics is a quantity that measures the effect of a force applied to a body for a certain interval of time.
We can also say the following.
Let's consider a force F acting on a body of mass m for a short interval of time dt. The instantaneous impulse of the force F is defined as the quantity dJ such that:
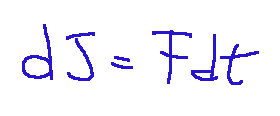
or also:
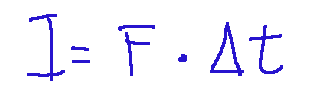
Where:
I = impulse (measured in Newtons per second,𝑁⋅𝑠)
F = the applied force (Newton,𝑁)
Δt = time interval during which the force acts (seconds,𝑠)
study of the motion of multiple point bodies
The dynamics of systems of material points deals with the study of the motion and interaction of multiple point bodies, useful for understanding the behavior of complex physical systems, in which multiple bodies interact with each other through forces.
In the dynamics of systems of material points, the laws of the dynamics of the point and the fundamental principles of physics are used to analyze the motion and interaction of bodies within the system.
And in these studies, one of the fundamental principles is precisely the principle of conservation of momentum, according to which the sum of the moments (mass times velocity) of the initial bodies is equal to the sum of the moments of the final bodies, provided that there are no external forces acting on the system. This principle allows us to understand how the motion of a body can influence the motion of other bodies in the system.
Conclusions
Studying momentum is fundamental in physics because it helps to understand the behavior of bodies in motion and the interactions between objects.
Question
The concept of momentum is a very old concept that has deep roots in scientific history, but did you know that the first to propose a modern and clear study of momentum was René Descartes (Cartesio), the French mathematician who created the system of Cartesian axes?

ITALIAN

11-04-2025 - Fisica - Quantità di moto [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_79-78)
Quantità di moto

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Si definisce quantità di moto e si indica con 𝒑, il prodotto tra la
massa (m) e la velocità (v) di un corpo secondo la relazione mostrata qui di seguito:
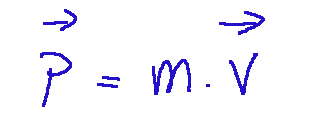
Dove:
p = quantità di moto
m = la massa (espressa in kg)
v = la velocità (espressa in m/s)
La quantità di moto è una grandezza vettoriale che riveste una particolare importanza quando si trattano gli urti tra i corpi ed è tale da consentire di prevedere modulo, direzione e verso della velocità dei corpi dopo l'urto. Ad esempio, il guard rail ai bordi di una strada deve essere in grado di rallentare e fermare il moto di un'automobile che sbanda e va fuori strada.
Unità di misura
L'unità di misura della quantità di moto nel Sistema Internazionale (SI) è il chilogrammo metro al secondo.
Questa unità di misura possiamo anche dedurla analizzando in due passaggi la formula della quantità di moto espressa prima.
primo passaggio
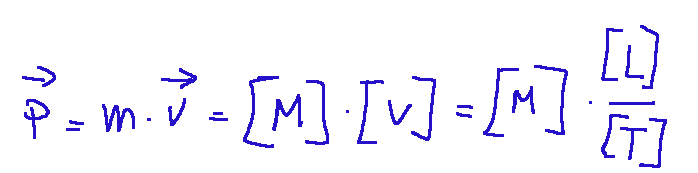
secondo passaggio
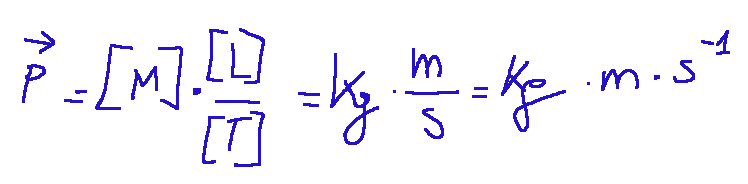
Conservazione della quantità di moto
Cosa succede quando due corpi sbattono l'uno contro l'altro?
Ipotizziamo il caso di due corpi di massa A e B che interagiscono tra di loro considerando una forza ad esempio attrattiva o repulsiva (di natura interna al sistema che stiamo considerando quella cioè derivante dall'urto tra i corpi).
La forza che la massa A esercita sulla massa B sarà FAB mentre la forza che massa B esercita sulla massa A sarà FBA. Per il terzo principio della dinamica sappiamo che le due forze saranno uguali in modulo e direzione ma di verso opposto così che la loro somma vettoriale è nulla:

Cosa dice in maniera sintetica il principio di conservazione della quantità di moto?
In un sistema isolato, la quantità di moto totale si conserva, cioè rimane costante nel tempo, anche se i singoli corpi che lo compongono cambiano velocità o direzione
Tenendo conto che due corpi A e B interagiscono (per esempio in una collisione), sappiamo che l'equazione del principio di conservazione della quantità di moto è la seguente:
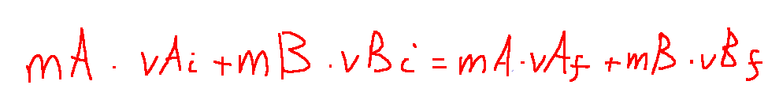
Scritta in questo modo, sembra una formula piuttosto complessa, ma in realtà non lo è, poiché basta sapere che:
m = massa del corpo
vi = velocità iniziale
vf = velocità finale
Da questa formula possiamo dedurre che la somma della quantità di moto prima dell’urto è uguale alla somma dopo.
Per quanto riguarda questo argomento possiamo dare anche una descrizione letterale più tecnica che può essere la seguente:
Possiamo affermare che il principio di conservazione della quantità di moto: quando la risultante delle forze esterne applicate ad un sistema è nulla, cioè quando il sistema è isolato, la quantità di moto si conserva nel tempo cioè assume sempre lo stesso valore. Dunque la variazione di quantità di
moto in un certo intervallo di tempo è sempre pari a 0.
NOTA: Generalmente, la quantità di moto si calcola considerando costante
la massa del corpo. Tuttavia anche la massa di un corpo può variare. Quindi, in alcuni problemi fisici devo considerarla variabile.
Gli scienziati della quantità di moto

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Gli scienziati che hanno studiato la quantità di moto sono persone molto note nel campo della storia scientifica. Ecco qui un elenco degli scienziati che hanno contribuito agli studi della quantità di moto:
-Galileo Galilei (1564–1642)
-René Descartes (Cartesio)
-Isaac Newton
-Leonhard Euler
-Emmy Noether
Impulso di una forza
L'impulso di una forza in fisica è una grandezza che misura l'effetto di una forza applicata su un corpo per un certo intervallo di tempo.
Possiamo dire anche quanto segue.
Consideriamo una forza F agente su un corpo di massa m per un breve intervallo di tempo dt. Si definisce impulso istantaneo della forza F, la grandezza dJ tale che:
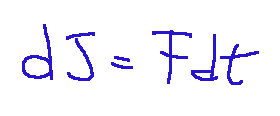
o anche:
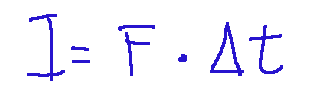
Dove:
I = impulso (misurato in Newton per secondo,𝑁⋅𝑠)
F = la forza applicata (Newton,𝑁)
Δt = intervallo di tempo durante il quale la forza agisce (secondi,𝑠)
studio del moto di più corpi puntiformi
La dinamica dei sistemi di punti materiali si occupa dello studio del moto e dell'interazione di più corpi puntiformi, utile a comprendere il comportamento dei sistemi fisici complessi, in cui più corpi interagiscono tra loro attraverso forze.
Nella dinamica dei sistemi di punti materiali, vengono utilizzate le leggi della dinamica del punto e i principi fondamentali della fisica per analizzare il moto e l'interazione dei corpi all'interno del sistema.
Ed in questi studi, uno dei principi fondamentali, è proprio il principio di conservazione della quantità di moto, secondo il quale la somma dei momenti (massa per velocità) dei corpi iniziali è uguale alla somma dei momenti dei corpi finali, a condizione che non ci siano forze esterne che agiscano sul sistema. Questo principio ci permette di capire come il moto di un corpo può influenzare il moto degli altri corpi nel sistema.
Conclusioni
Studiare la quantità di moto è fondamentale in fisica perché aiuta a comprendere il comportamento dei corpi in movimento e le interazioni tra oggetti.
Domanda
Il concetto di quantità di moto è un concetto molto antico che ha radici profonde nella storia scientifica, ma lo sapevate che il primo a proporre uno studio moderno e chiaro della quantità di moto fu René Descartes (Cartesio), cioè il matematico francese che ideò il sistema di assi cartesiani?
THE END
