~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
08-02-2024 - Physics - Partition wall with multiple screens [EN]-[IT]
Dividing wall with multiple screens
Basic concepts
In thermodynamics the equations of state are fundamental, below is an example.
We will see one of the fundamental relations, the equation of state of ideal gases. Here it is shown below,
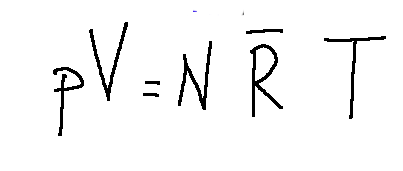
Where:
p = pressure
V = volume
N = number of kilomoles
R = universal gas constant which is equal to 8314 [Pam3/kmol°K]
T = temperature
When we talk about perfect gases we must introduce the concept of the specific heat of the gas at constant volume.
The definition of specific heat is as follows.
Specific heat measures the heat needed to raise the temperature of one kilogram of substance by one degree.
If n moles of a gas at constant volume are heated by an infinitesimal increase in temperature dT, the necessary heat is given by the following formula:
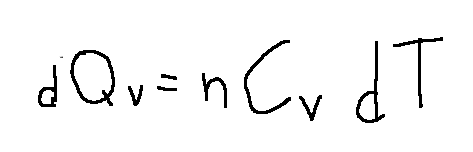
if we think that p/T is a function only of the volume (V)
we can write the following relationship that resembles the one above.
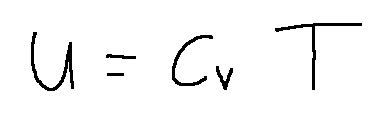
This is also called ideal gas equation of state
IMPORTANT:
The specific heat Cv depends on the gas.
The link below takes you to a site where there is a table with the specific heats of some materials.
The behavior of a system in which a gas is present can be described with two equations. This is a necessary condition as there are two degrees of freedom in the system, i.e. u and v.
For ideal gases there is a fundamental relationship which is the following:
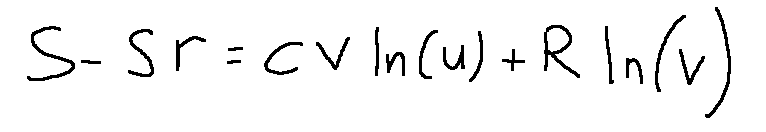
how insulation varies with different screens
To better understand what happens to the insulation by applying multiple screens to a partition wall, let's start by comparing the resistivity of a masonry wall and a sheet of glass.
Remember that thermal resistance is the difficulty heat has in passing through a medium. This can be a solid, a liquid or a gas.
Let's consider:
-a masonry wall with a thickness of 30 cm and a k of 1W/m°K
-a glass plate with a thickness of 4 millimeters and a k= 1 W/m°K
We always think of the system with the analogy of an electrical diagram.
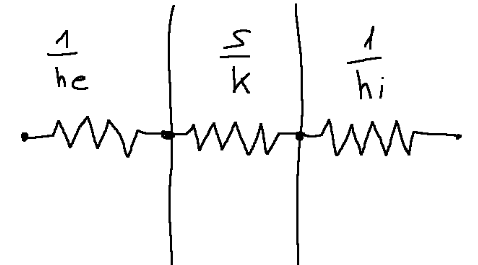
WHERE:
he is external h which can be forced convection like wind and we consider a value of 14
hi is internal h which is natural convection and we consider a value of 7
Let's take the following formula to calculate the resistivity of the wall and glass
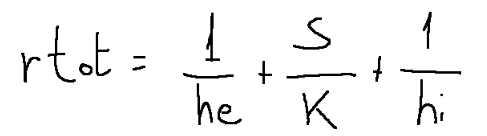
WHERE:
S is the thickness
k = thermal conductivity which identifies the behavior of different materials regarding heat transmission and is measured in W/m K
If we proceed with the calculations we find that the resistivity of the wall is 0.5 m2·°K/W while that of the glass is 0.2 m2·°K/W.
We note that the resistivity of the glass is just under half that of the wall,
If you add more screens, like N screens, the heat transfer behavior will be related to the following formula.
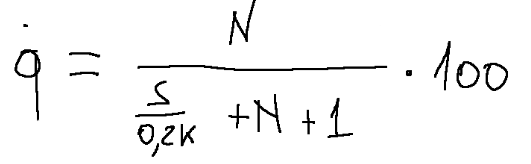
curve of the wall
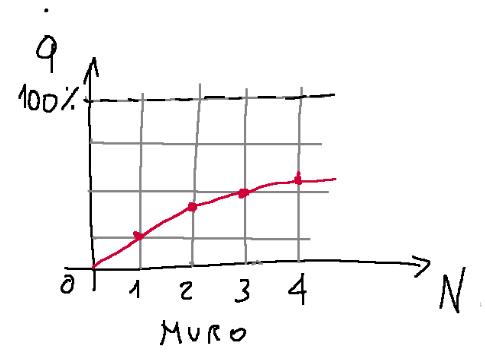
Conclusions
From the relationship above we understand that the behaviors are different depending on the materials we use as they have different k.
The other thing that is understood is that if we add two screens to the wall the curve does not double. The thermal resistivity condition improves but is not directly proportional to the added screens.
Request
Did you know that in an insulation system the benefit of the third and fourth screen is always less than the benefit of the first and second screen.

08-02-2024 - Fisica - Parete divisoria con più schermi [EN]-[IT]
Parete divisoria con più schermi
Concetti base
Nella termodinamica le equazioni di stato sono fondamentali, qui di seguito un esempio.
Vedremo una delle relazioni fondamentali, l'equazione di stato dei gas perfetti. Eccola mostrata qui di seguito,
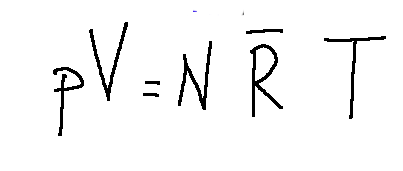
Dove:
p = pressione
V = volume
N = numero di kilomoli
R = costante universale dei gas che vale 8314 [Pam3/kmol°K]
T = temperatura
Quando si parla di gas perfetti dobbiamo introdurre il concetto del calore specifico del gas a volume costante.
La definizione di calore specifico è la seguente.
Il calore specifico misura il calore che è necessario per far incrementare di un grado la temperatura un chilogrammo di sostanza,
Se si scaldano n moli di un gas a volume costante di un incremento infinitesimo di temperatura dT, il calore necessario è dato dalla seguente formula:
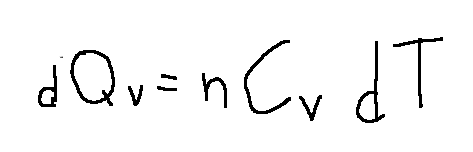
se pensiamo che p/T è funzione solo del volume (V)
possiamo scrivere la seguente relazione che assomiglia a quella riportata qui sopra.
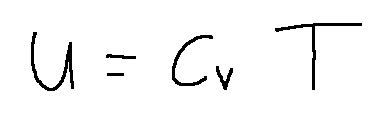
Questa è chiamata anche equazione di stato per i gas perfetti
IMPORTANTE:
IL calore specifico Cv dipende dal gas.
Il link qui sotto segnalato vi porta in un sito dove è presente una tabella con dei calori specifici di alcuni materiali.
Il comportamento di un sistema in cui è presente un gas può essere descritto con due equazioni. Questa è una condizione necessaria in quanto ci sono due gradi di libertà del sistema, cioè u e v.
Per i gas perfetti esiste una relazione fondamentale che è la seguente:
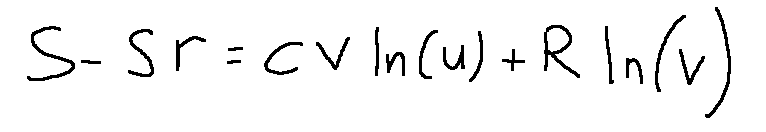
come varia la coibentazione al variare degli schermi
Per comprendere meglio cosa succede alla coibentazione applicando più schermi ad una parete divisoria cominciamo con il confrontare la resistività di una parete in muratura e una lastra di vetro.
Si ricorda che la resistenza termica è la difficoltà che ha ill calore nell'attraversare un mezzo. Questo può essere un solido, un liquido o un gas.
Consideriamo:
-una parete in muratura con spessore 30 cm ed un k di 1W/m°K
-una lastra di vetro con spessore 4 millimetri ed un k= 1 W/m°K
Pensiamo al sistema sempre con l'analogia di uno schema elettrico.

DOVE:
he è h esterno che può essere convezione forzata come il vento e consideriamo un valore di 14
hi è h interno che è la convezione naturale e consideriamo un valore di 7
Prendiamo la seguente formula per calcolare la resistività del muro e del vetro
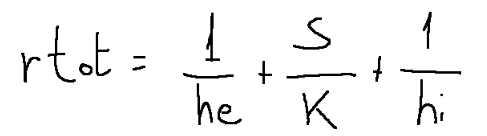
DOVE:
S è lo spessore
k = conducibilità termica che identifica il comportamento dei diversi materiali riguardo alla trasmissione del calore e si misura in W/m K
Se procediamo con i calcoli abbiamo che la resistività del muro è 0,5 m2·°K/W mentre quella del vetro è 0,2 m2·°K/W.
Notiamo che la resistività del vetro è poco meno della metà di quella della parete,
Se si aggiungono più schermi, tipo N schermi, il comportamento del trasferimento del calore sarà in relazione alla seguente formula.
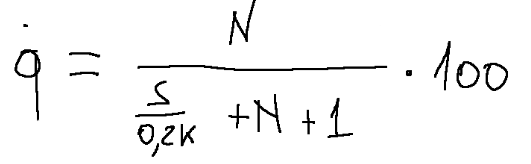
curva del muro

Conclusioni
Dalla relazione qui sopra comprendiamo che i comportamenti sono differenti a seconda dei materiali che usiamo in quanto hanno k diversi.
L’altra cosa che viene compresa è che se aggiungiamo due schermi al muro la curva non raddoppia. La condizione della resistività termica migliora ma non è direttamente proporzionale agli schermi aggiunti.
Domanda
Sapevate che in un sistema di coibentazione il beneficio del terzo e quarto schermo è sempre inferiore al beneficio del primo e secondo schermo.
THE END