~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

07-07-2025 - Mathematical Analysis - Asymptotes [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-78)
Asymptotes
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
When we talk about asymptote we must think of a function or even better the graph of a function. The asymptote is a straight line to which the graph of a function approaches indefinitely without ever touching the asymptote.
Basically the function approaches the line, that is, the values of the function approach the line, but the distance between the values of the function and the asymptote will never be equal to zero
Calculating asymptotes
By calculating the limits of a function, the asymptotes can be determined, which in other words are those lines such that the distance between them and the graph of the function tends to 0 for x that tends to a point where the function is not defined or is not continuous or for x that tends to + or - (∞) infinity
Examples of asymptotes
Horizontal asymptote
Here is a condition classic
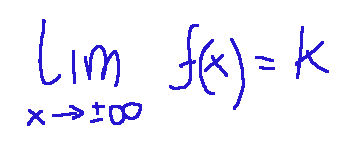
Here is a classic example:
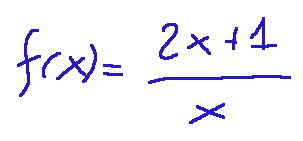
Here is the graph where we note that y = 2
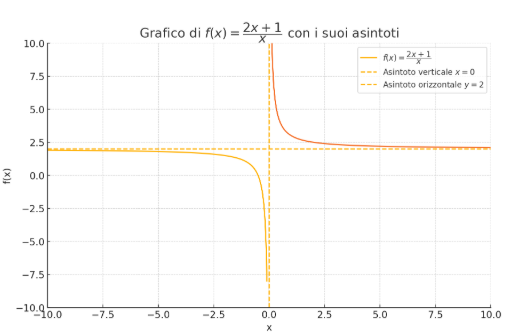
image created with artificial intelligence, the software used is ChatGPT
Vertical asymptote
Here is a classic condition
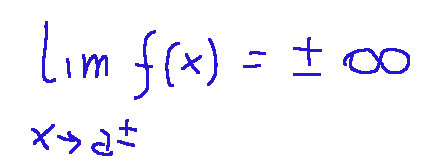
Here is an example classic:
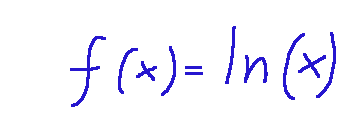
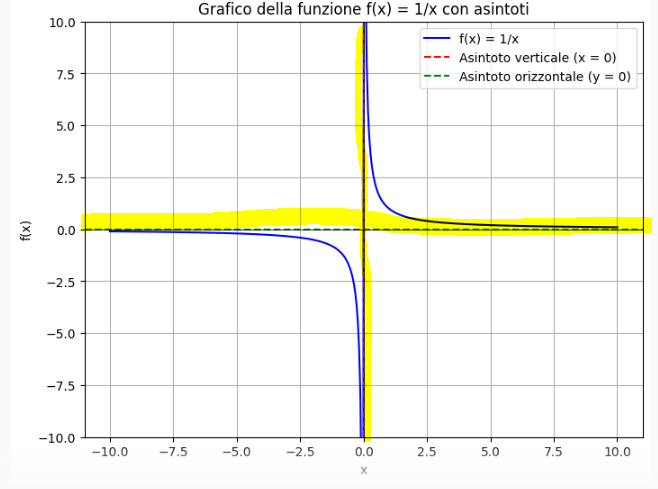
Below is the graph where we note that x = 0
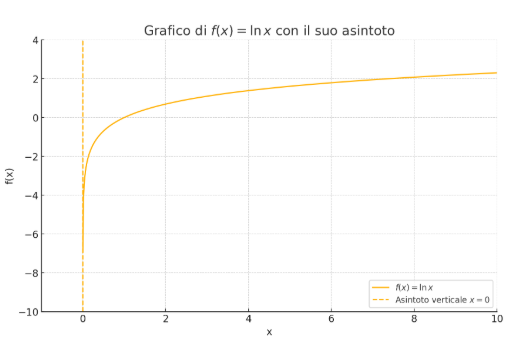
image created with artificial intelligence, the software used is ChatGPT
Asymptote oblique
Let's now take one of the special cases, where the asymptote is neither vertical nor horizontal, but oblique.
One of the functions that has an oblique asymptote is the following:
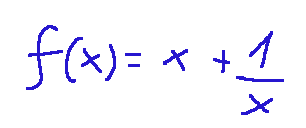
Below is the graph of the function
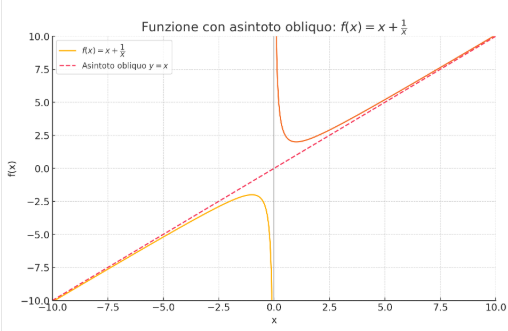
I consider this the most classic example of an oblique asymptote in which the asymptote line is x=y.
Notice that the two branches of the function get closer and closer to the line y=x as the absolute value of x becomes larger and larger.
Conclusions
An asymptote is an imaginary line in which the values of a given function get close to, but never touch that line. Their study is important in the field of mechanical design, optical design and error control on models.
Question
Even though the term "function" was coined by Leibniz in 1694, functions were already studied in some way in the past. Did you know that the first person who left an explicit trace of some studies on asymptotes was the Greek mathematician Apollonius of Perga (about 262–190 BC)? Did you know that Apollonius himself, called in his time "the Great Geometer", forged the names: ellipse, parabola and hyperbola?Bold

ITALIAN

07-07-2025 - Analisi Matematica - Asintoti [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-78)
Asintoti

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Quando parliamo di asintoto dobbiamo pensare ad una funzione o ancora meglio al grafico di una funzione. L'asintoto è una retta alla quale il grafico di una funzione si avvicina indefinitamente senza mai toccare l'asintoto.
Sostanzialmente la funzione si avvicina alla retta, cioè i valori della funzione si avvicinano alla retta, ma la distanza tra i valori della funzione e l'asintoto non sarà mai uguale a zero
Il calcolo degli asintoti
Mediante il calcolo dei limiti di una funzione, si possono determinare gli asintoti, che in altre parole sono quelle rette tali che la distanza tra esse e il grafico della funzione tende a 0 per x che tende ad un punto ove la funzione non è definita o non è continua o per x che tende a + o - (∞) infinto
Esempi di asintoti
Asintoto orizzontale
Qui di seguito una condizione classica
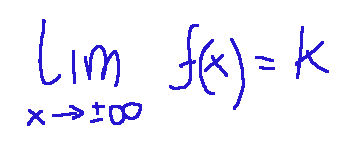
Qui di seguito un esempio classico:
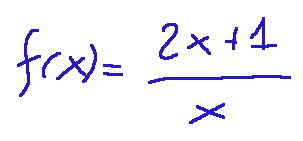
Qui di seguito il grafico dove notiamo che ha y = 2

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Asintoto verticale
Qui di seguito una condizione classica
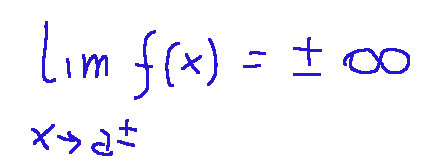
Qui di seguito un esempio classico:
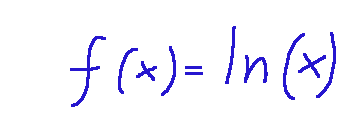
Qui di seguito il grafico dove notiamo che ha x = 0

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Asintoto obliquo
Prendiamo ora uno dei casi particolari, dove l'asintoto non è nè verticale nè orizzontale, ma obliquo.
Una delle funzioni che ha un asintoto obliquo è la seguente:
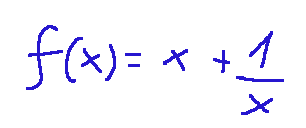
qui di seguito il grafico della funzine

Questo lo considero l'esempio più classico di un asintoto obliquo in cui la retta dell'asintoto è x=y.
Notiamo che i due rami della funzione si avvicinano sempre di più alla retta y=x quando il valore assoluto di x diventa sempre più grande.
Conclusioni
Un asintoto è una linea immaginaria in cui i valori di una determinata funzione si avvicinano, ma non toccano mai quella retta. Il loro studio è importante nel campo della progettazione meccanica, della progettazione ottica e nel controllo di errori su modelli.
Domanda
Anche se il termine "funzione" fu coniato da Leibniz nel 1694, le funzioni in qualche modo erano già studiate in passato. Lo sapevate che il primo che ha lasciato una traccia esplicita di alcuni studi sugli asintoti fu il matematico greco Apollonio di Perga (circa 262–190 a.C.)? Lo sapevate che proprio Apollonio, chiamato a suo tempo "il Grande Geometra", ha forgiare i nomi: ellisse, parabola e iperbole?
THE END