~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

02-07-2025 - Mathematical Analysis - Neper's Number [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-81)
Neper's Number

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
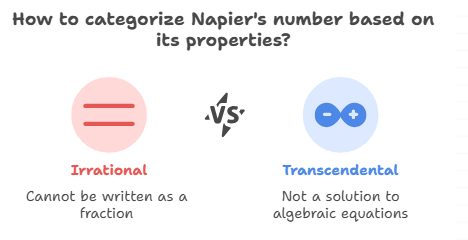
image created with artificial intelligence, the software used is Napkin.ai
Napier's number is usually indicated with the letter e and is approximately 2.718281828
This number has two main characteristics
-Irrational, that is, it cannot be written as a fraction
-Transcendental, that is, it is not the solution of any algebraic equation with rational coefficients.
It is the base of natural logarithms.
Classical definition of Napier's number
The limit shown below is one of the most classical definitions of Napier's number.
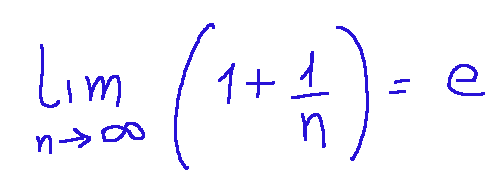
Napier's number is important for 5 main reasons:
1-it is the base of natural logarithms
2-Derivative of the exponential function. The e^x function is the only one with a derivative equal to itself
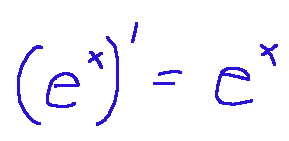
3-Continuous compound interest
4-Developments and series
5-Notable limit for calculations.
The natural logarithm
The natural logarithm is the logarithm to the base e, that is, the logarithm to the base of Napier's number. Essentially, the natural logarithm of a positive number x is the exponent to which e must be raised to obtain precisely x.
We can express this concept mathematically as follows:

In simple terms the natural logarithm is the inverse function of the exponential e^x
here is the graph of the natural logarithm
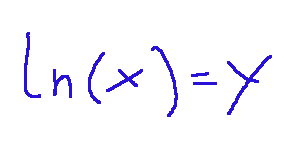
here it is below
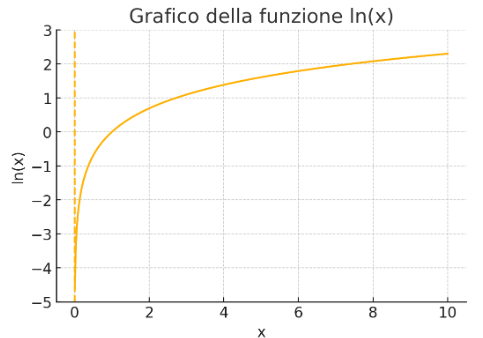
image created with artificial intelligence, the software used is ChatGPT
In this graph we note that:
The vertical asymptote in x is equal to 0+ and we note that the value drops to -∞
It passes through (1,0), in fact ln 1 = 0 (the natural logarithm of 1 is equal to zero)
Example
What is the value of the following limit?
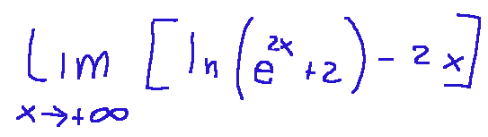
development
Let's start doing the various transformations
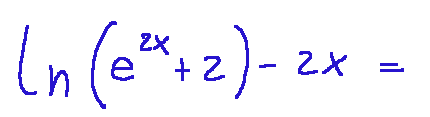

since...

we get the following
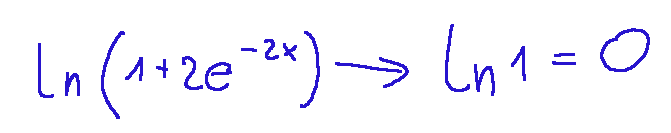
Result
The limit as x tends to +∞ of [ln(e2x+2)-2x]
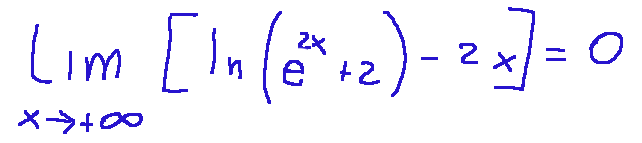
is exactly 0
Conclusions
The fundamental definition of the number of Napier is the following:
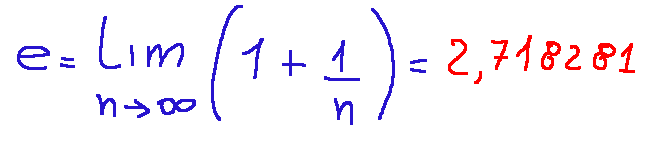
We can conclude this post by saying that e (Napier's number) is the constant that makes the description of any phenomenon related to growth, decay, continuity and periodicity natural.
Question
Did you know that the Scottish mathematician, astronomer and physicist John Napier (1550-1617), known as Napier, was the first to introduce the concept of the natural logarithm?

ITALIAN

02-07-2025 - Analisi Matematica - Il numero di Nepero [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-81)
Il numero di Nepero

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione

immagine creata con l’intelligenza artificiale, il software usato è Napkin.ai
Il numero di Nepero è solitamente indicato con la lettera e e vale circa 2,718281828
Questo numero ha due caratteristi principali
-Irrazionale, cioè non si può scrivere come frazione
-Trascendente, cioè non è soluzione di nessuna equazione algebrica a coefficienti razionali.
Esso è la base dei logaritmi naturali.
Definizione classica del numero di Nepero
Il limite mostrato qui sotto è una delle definizioni più classiche del numero di Nepero.
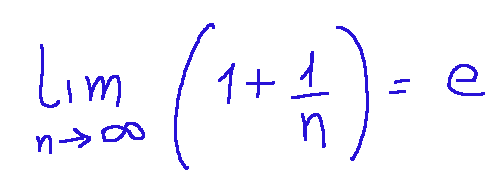
Il numero di Nepero è importante per 5 motivi principali:
1-è la base dei logaritmi naturali
2-Derivata della funzione esponenziale. La funzione e^x è l'unica con derivata uguale a se stessa
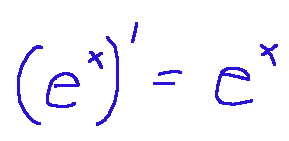
3-Interesse composto continuo
4-Sviluppi e serie
5-Limite notevole per calcoli.
Il logaritmo naturale
Il logaritmo naturale è il logaritmo in base e, cioè il logaritmo in base al numero di Nepero. Sostanzialmente il logaritmo naturale di un numero positivo x è l'asponente a cui bisgona elevare e per ottenere proprio x.
Possiamo esprimere matematicamente questo concetto come segue:

In parole semplici il logaritmo naturale è la funzione inversa dell'esponenziale e^x
qui di seguito il grafico del logaritmo naturale
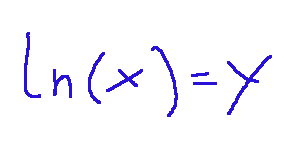
eccolo qui sotto

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
In questo grafico notiamo che:
L'asintoto verticale in x è uguale a 0+ e notiamo che il valore scende a -∞
Passa per (1,0), infatti ln 1 = 0 (il logaritmo naturale di 1 è uguale a zero)
Esempio
Quanto vale il seguente limite?
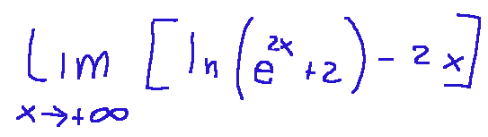
sviluppo
Iniziamo a fare le varie trasformazioni
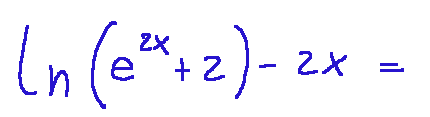
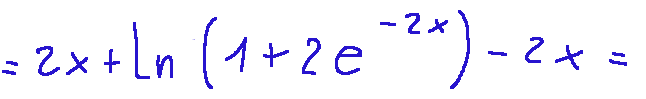
siccome...

otteniamo quanto segue
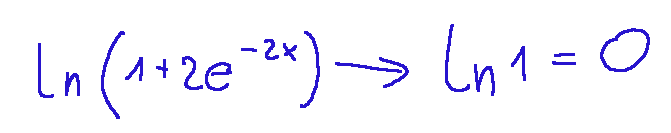
Risultato
Il limite per x che tende a +∞ di [ln(e2x+2)-2x]
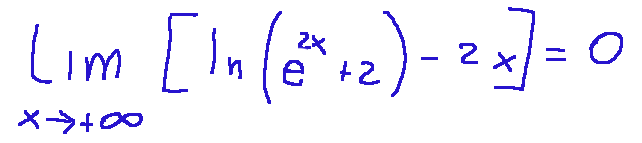
vale esattamente 0
Conclusioni
La definizione fondamentale del numero di Nepero è la seguente:
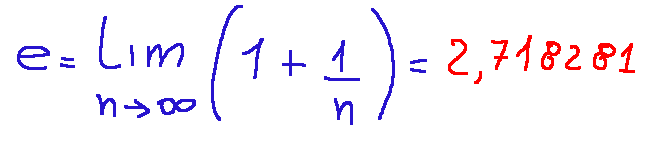
Possiamo concludere questo post dicendo che e (il numero di Nepero) è la costante che rende naturale la descrizione di qualsiasi fenomeno legato alla crescita, al decadimento, alla continuità e alla periodicità.
Domanda
Lo sapevate che il matematico, astronomo e fisico scozzese John Napier (1550-1617), conosciuto come Nepero, fu il primo ad introdurre il concetto del logaritmo naturale?
THE END
