
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
01-12-2024 - Analytic Geometry - Algebraic Surfaces [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_54)
Algebraic Surfaces
Definition
Algebraic surfaces in space are the natural generalization of planes, and are obtained by increasing the degree of the polynomials that define them.
Formal Definition
An algebraic surface is the locus of points in three-dimensional space (x,y,z) that satisfy an equation of the following form:

where f(x,y,z) is a polynomial in three variables with real or complex coefficients.
Spheres
A sphere with center C and radius r>0 is the set of points that have distance r from C.

Using the Cartesian reference system (O; x,y,z) we can write an implicit formula that represents the sphere with center C and radius r.
The following equation represents a sphere:

So the equation can also be written as follows:

which represents a sphere with center C and radius r represented as continues
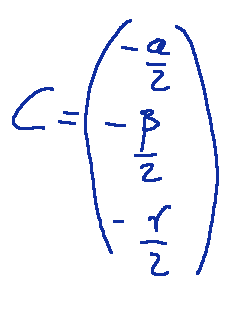

Cones
A cone is the set of points such that there exists a Cartesian reference system (O;x, y, z) with respect to which they are the solutions of the equation next
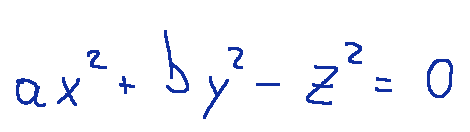
The point O is called the vertex of the cone, while the z-axis is called the axis of the cone.
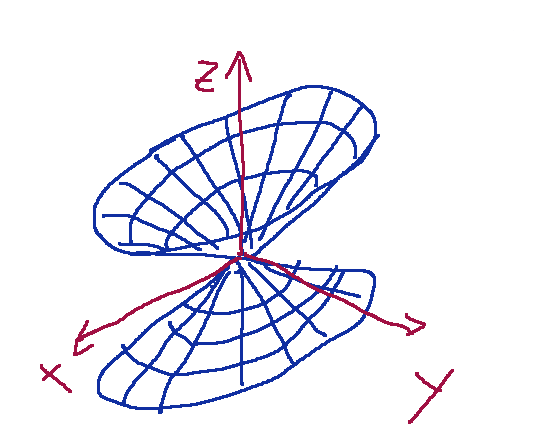
Conclusions
Algebraic surfaces are a fundamental concept of analytic geometry and algebraic geometry. These are surfaces defined as sets of points in the three-dimensional space R3 or C3 that satisfy a polynomial equation of finite degree.
Question
In my opinion, translating algebraic surfaces into algebraic equations has always been something complex, what do you think?

[ITALIAN]
01-12-2024 - Geometria analitica - Superfici algebriche [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_54)
Superfici algebriche
Definizione
Le superfici algebriche nello spazio sono la naturale generalizzazione dei piani, e sono ottenute aumentando il grado dei polinomi che le definiscono.
Definizione formale
Una superficie algebrica è il luogo dei punti nello spazio tridimensionale (x,y,z) che soddisfano un’equazione dalla seguente forma:

dove f(x,y,z) è un polinomio in tre variabili con coefficienti reali o complessi.
Sfere
Una sfera con centro C e raggio r>0 è l’insieme dei punti che hanno distanza r da C.

Usando il sistema di riferimento cartesiano (O; x,y,z) possiamo scrivere una formula implicita che rappresenta la sfera con centro C e raggio r.
L’equazione seguente rappresenta una sfera:

Quindi l’equazione può essere scritta anche come segue:

che rappresenta una sfera con centro C e raggio r rappresentati come segue
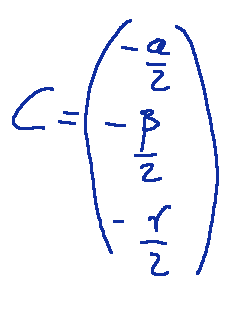

Coni
Un cono è l’insieme dei punti tali che esiste un sistema di riferimento cartesiano (O;x, y, z) rispetto al quale essi sono le soluzioni dell’equazione seguente
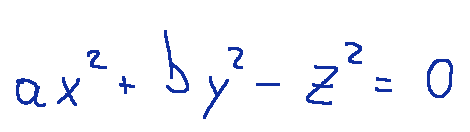
Il punto O è detto vertice del cono, mentre l’asse z è detto asse del cono.

Conclusioni
Le superfici algebriche sono un concetto fondamentale della geometria analitica e della geometria algebrica. Si tratta di superfici definite come insiemi di punti nello spazio tridimensionale R3 o C3 che soddisfano un'equazione polinomiale di grado finito.
Domanda
Secondo me tradurre in equazioni algebriche le superfici algebriche è sempre stato qualcosa di complesso, voi come la pensate?
THE END



