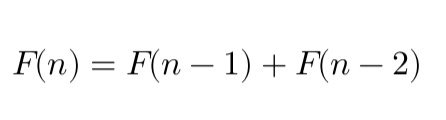~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

01-07-2025 - Mathematical Analysis - Sequences [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-83-82)
Sequences

image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
A real sequence is a function...

where:
D = N
Real sequence
A function that assigns to every natural number a real number is called a real sequence.
Mathematically we can express it as follows:

We can simply say that it is an infinite sequence of real numbers.
Let's remember that real numbers are:
-Natural numbers
-Integer numbers
-Rational numbers
-Finite or periodic decimal numbers
-Irrational numbers (π, e, √2, etc...etc...)
Regular sequence
A regular sequence, also called monotonically increasing, is simply a real sequence that never decreases.
Mathematically we can describe it like this:

Every regular sequence has a unique limit.
Every monotone sequence is regular and convergent if bounded
Example
Let's take the following sequence as an example and think that it is convergence, so what happens?

We have a sequence of differences:

this series is convergent and therefore there exists a limit:

Essentially, the sequence, from the point of view of the sign of its increments, stabilizes. So the oscillation is impossible.

image created with artificial intelligence, the software used is ChatGPT
So we come to the conclusion that an cannot oscillate
Study of a sequence
Let's take the following succession

the first thing we can do is compare the growth by examining an with an+1, which mathematically means.

Let's calculate the sequence, so we will arrive at the following mathematical conclusion:

From this mathematical relation we can see that the sequence is increasing.
We see that with n=2, n=3 and n=4, we have the following results -1/2, -1/6, -1/12
The expression tends to 0 from negative values as n increases.
limitation
Now consider the limit for n-->∞

The more n increases, the more the fraction 1/n-1 decreases, the terms decrease towards 1
Below is the graph of the sequence:

graph below

image created with artificial intelligence, the software used is ChatGPT
result
We can say that this sequence is decreasing and limited. For n=1 the sequence is not defined.
Conclusions
Sequences are part of the foundations of mathematical analysis. Sequences are used to define limits, continuity, derivatives, integrals in R. All these things can be formulated through sequences. Furthermore, sequences are used to "draw" or better to say, understand, decay chains or orbits in computational mechanics.
Question
It was Leonardo Fibonacci in the 13th century who introduced one of the most famous series in the world, his famous Fibonacci sequence. Did you know that the Fibonacci sequence appears in nature? The arrangement of petals in flowers, leaves on the stem and the shape of shells follow the Fibonacci series.

ITALIAN

01-07-2025 - Analisi Matematica - Successioni [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-83-82)
Successioni

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Una successione reale è una funzione...

dove:
D = N
Successione reale
Una funzione che assegna a ogni numero naturale un numero reale viene definita come successione reale.
Matematicamente possiamo esprimerlo come segue:

Semplicemente possiamo dire che è una sequenza infinita di numeri reali.
Ricordiamo che i numeri reali sono:
-Numeri naturali
-Numeri interi
-Numeri razionali
-Numeri decimali finiti o periodici
-Numeri irrazionali (π, e, √2, ecc...ecc...)
Successione regolare
Una successione regolare, detta anche monotona crescente, è semplicemente una successione reale che non diminuisce mai.
Matematicamente la possiamo descrivere così:

Ogni successione regolare ammette un unico limite.
Ogni successione monotona è regolare ed è convergente se limitata
Esempio
Prendiamo come esempio la successione seguente e pensiamo che sia convergenza, quindi cosa succede?

Abbiamo una successione delle differenza:

questa serie è convergente e quindi esiste un limite:

Sostanzialmente, la successione, dal punto di vista del segno dei suoi incrementi, si stabilizza. Quindi l'oscillazione è impossibile.

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Quindi arriviamo alla conclusione che an non può oscillare
Studio di una successione
Prendiamo la seguente successione

la prima cosa che possiamo fare è confrontare la crescita andando ad esaminare an con an+1, che matematicamente significa.

Andiamo a calcolare la successione, quindi arriveremo alla seguente conclusione matematica:

Da questa relazione matematica possiamo notare che la successione è crescente.
Vediamo che con n=2, n=3 e n=4, abbiamo i seguenti risultati -1/2, -1/6, -1/12
L'espressione tende a 0 da valori negativi man mano che cresce n.
limitatezza
Consideriamo ora il limite per n-->∞

Più n cresce e più la frazione 1/n-1 diminuisce, i termini decrescono verso 1
Qui di seguito il grafico della successione:

grafico qui sotto

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
risultato
Possiamo dire che questa successione è decrescente e limitata. Per n=1 la successione non è definita.
Conclusioni
Le successioni fanno parte delle fondamenta dell'analisi matematica. Le successioni servono nel definire i limiti, la continuità, la derivata, gli integrali in R. Tutte queste cose possono essere formulate tramite successioni. Inoltre le successioni servono per "disegnare" o meglio dire, comprendere, le catene di decadimento o le orbite in meccanica computazionale.
Domanda
Fu Leonardo Fibonacci nel XIII secolo ad introdurre una delle serie più famose al mondo, la sua celebre successione di Fibonacci. Lo sapevate che la successione di Fibonacci compare in natura? La disposizione dei petali nei fiori, delle foglie sullo stelo e la forma delle conchiglie seguono la serie di Fibonacci.
THE END