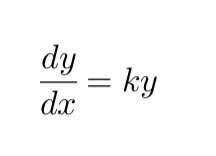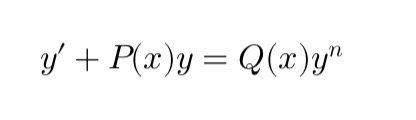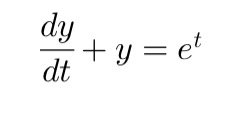~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

16-07-2025 - Mathematical Analysis - Types of Differential Equations [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic mentioned above.
(code notes: X-44-43-42-41)
Types of Differential Equations
Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Equations are mathematical expressions that establish a relationship between two quantities. Essentially, it's as if they balanced the two terms, one on the left of the equals sign and the other on the right.
Differential equations, on the other hand, involve one or more derivatives of a function; in a less complicated way, we can say that they indicate something that varies. This particular mathematical tool is used to describe physical, economic, or biological phenomena that change over time.
Before continuing, I warn you that from here on out there will be some rather technical explanations, and I'm thinking of revisiting these topics in the future, but only partially and with more extensive explanations, including the basic concepts. However, I didn't do that this time. For those without a basic understanding, I warn you that it might get boring.
First-Order Linear Differential Equations
A first-order differential equation is said to be linear if it can be written in the form shown below.
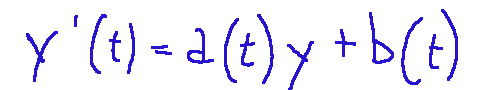
I'll try to explain it another way, using different words and going step by step.
A first-order differential equation contains the first derivative of an unknown function y(x).
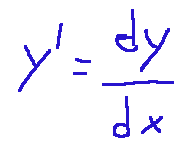
It is also defined as linear when y and y' appear only at the first degree, that is, there are no powers, products between them, or nonlinear functions of y.
Below we translate mathematically what has just been expressed.
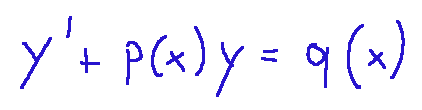
WHERE:
p(c) and q(x) are known functions of x
NOTE: If q(x)=0, the equation is homogeneous; otherwise, it is defined as non-homogeneous, but I'll discuss this later.
Where are they used?
First-order linear differential equations are used to describe the evolution of a quantity whose variation is proportional to its current value. They are used in finance, macroeconomics, and chemistry.
Nth-order linear differential equations
We've seen first-order linear differential equations; now let's move on to the next difficulty.
Linear differential equations of order n in normal form look like this.
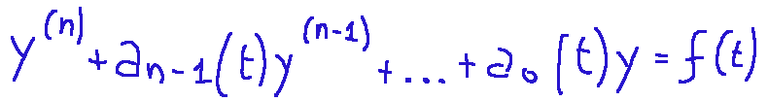
Let me try to put it another way.
An nth-order linear differential equation in a real variable x has the following form:
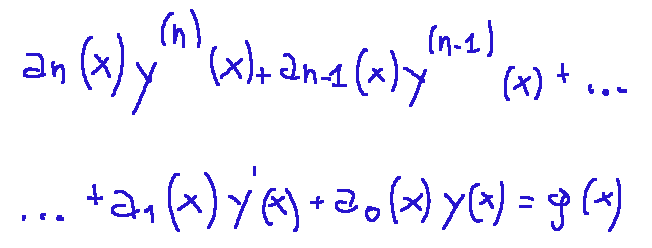
Where:
y^(k) = k-th derivative of y
ak(x) = known functions of x
Where are they used?
Nth-order linear differential equations are used to describe linear dynamic systems with n independent states. It is important to note that a linear differential equation of order n can describe any physical, technical, or economic system that is linear, time-invariant, and has n energy or information storage elements.
Homogeneous linear equation with constant coefficients
Below is what a homogeneous linear equation with constant coefficients looks like.
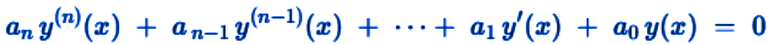
image created with artificial intelligence, the software used is ChatGPT
Below I show what a homogeneous linear equation with constant coefficients looks like with a concrete example.
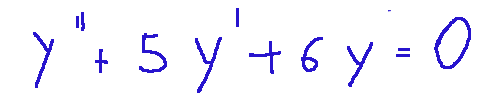
Non-homogeneous linear equation with constant coefficients
This is what a non-homogeneous linear equation with constant coefficients looks like.

The order of this equation is 2, with coefficients 3 and 2 being constants, the non-zero term e^x shows the non-homogeneity of the equation.
Conclusions
Differential equations are classified according to their order, whether they are ordinary or partial, whether they are linear or nonlinear, whether they are homogeneous or inhomogeneous, and whether they have constant or variable coefficients.
Question
Did you know that around 1700, Jakob and Johann Bernoulli applied transformations to differential equations that are still taught in a completely identical manner today?

ITALIAN

16-07-2025 - Analisi Matematica - Tipologie delle equazioni differenziali [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-44-43-42-41)
Tipologie delle equazioni differenziali
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Le equazioni sono delle espressioni matematiche che stabiliscono una relazione tra due quantità. Sostanzialmente è come se bilanciassero i due termine che stanno uno a sinistra dell'uguale e l'altro a destra.
Le equazioni differenziali invece coinvolgono una o più derivate di una funzione, in maniera meno complicata possiamo dire che indicano qualcosa che varia. Questo particolare strumento matematico viene usato per descrivere fenomeni fisici, economici o biologici che cambiano nel tempo.
Prima di proseguire, avverto che da qui in poi ci saranno delle spiegazioni piuttosto tecniche e sto pensando di riproporre in futuro questi argomenti, ma in maniera parziale e con spiegazioni più ampie riportando anche i concetti base. Però questa volta non l'ho fatto. Per chi non ha una conoscenza di base, avverto che potrebbe annoiarsi.
Equazioni differenziali lineari del primo ordine
Un equazione differenziale del primo ordine si definisce lineare se si può scrivere nella forma qui sotto riportata
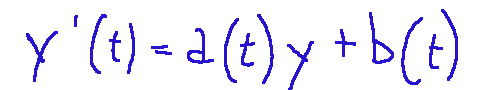
Provo a dare un altra spiegazione usando altre parole e andando per passi.
Un'equazione differenziale del primo ordine contiene la derivata prima di una funzione incognita y(x)
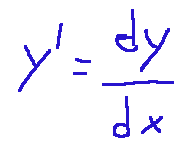
Si definisce invece, anche lineare quando y e y' compaiono solo al primo grado, cioè non ci sono potenze, prodotti tra loro o funzioni non lineari di y.
Qui di seguito traduciamo matematicamente quello che è stato appena espresso.
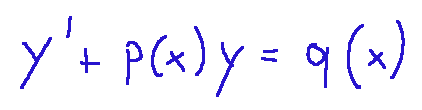
DOVE:
p(c) e q(x) sono funzioni note di x
NOTA: Se q(x)=0, l'equazione sarà omogenea, altrimenti verrà definita non omogenea, ma ne parlerò più avanti.
Dove si usano?
Le equazioni differenziali lineari del primo si usano per descrivere l’evoluzione di una grandezza la cui variazione è proporzionale al suo valore corrente. Vengono applicate in finanza, in macroeconomia ed in chimica.
Equazioni differenziali lineari di ordine n
Abbiamo visto le equazioni differenziali lineari del primo ordine ora passiamo ad una difficoltà successiva.
Le equazioni differenziali lineari di ordine n in forma normale appaiano come segue.
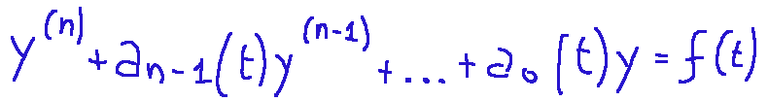
Provo a dirle in un altra maniera.
Una equazione differenziale lineare di ordine n in una variabile reale x ha la forma seguente:
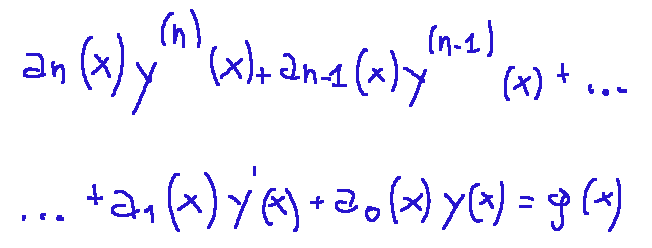
Dove:
y^(k) = derivata k-esima di y
ak(x) = funzioni note di x
Dove si usano?
Le equazioni differenziali lineari di ordine n si usano per descrivere sistemi lineari dinamici con n stati indipendenti. Bisogna sapere che un’equazione differenziale lineare di ordine n può descrivere qualunque sistema fisico, tecnico o economico che sia lineare, tempo-invariante e che disponga di n elementi d’accumulo di energia o informazione
Equazione lineare omogenea a coefficienti costanti
Qui di seguito ecco come appare un'equazione lineare omogenea a coefficienti costanti.
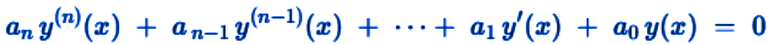
immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Qui di seguito mostro come appare con un esempio concreto un'equazione lineare omogenea a coefficienti costanti.
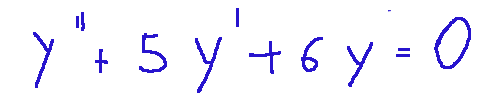
Equazione lineare non omogenea a coefficienti costanti
Ecco come appare un equazione lineare non omogenea a coefficienti costanti

L'ordine di questa equazione è 2, i coefficienti 3 e 2 sono costanti, il termine e^x diverso da zero, mostra la non omogeneità dell'equazione.
Conclusioni
Le equazioni differenziali si classificano a seconda dell'ordine, se sono ordinarie o parziali, se sono lineari o non lineari, se sono omogenee o non omogenee e se sono a coefficienti costanti o a coefficienti variabili.
Domanda
Lo sapevate che intorno al 1700 Jakob & Johann Bernoulli hanno applicato alcune trasformazioni alle equazioni differenziali che si insegnano ancora oggi in maniera completamente identica?
THE END