
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

13-04-2025 - Physics - Rotational motion and composition of motions [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_73-72)
Rotational motion and composition of motions

image created with artificial intelligence, the software used is Microsoft Copilot
the moment of inertia
The moment of inertia is usually represented with the letter I.
We can say that the moment of inertia of a body with mass M, approximated by a material point, turns out to be the product of the mass of the body by the squared distance from an axis around which the body rotates.
we can define it mathematically as follows.

We can also say that it represents how much position a body makes to the variation of its angular velocity of rotation around the axis. The unit of measurement of the moment of inertia in the international system is kg m^2
When we are faced with rigid bodies we must know that there are formulas to calculate the moment of inertia.
These formulas are present in some tables and describe the moments of inertia of the main forms of rigid bodies. These shapes can be the cylindrical shell, the full cylinder, the hollow cylinder, a rod, a spherical shell, a sphere or a parallelepiped.
Rotational kinetic energy
Now let's introduce the concept of rotational kinetic energy. Rotational kinetic energy is the energy associated with the rotational motion of a body around an axis. We can also say that this energy is the rotational equivalent of the classic kinetic energy that we use for rectilinear motion, only that in this case it concerns how much energy a body that is rotating has. The formula for rotational kinetic energy is written below.
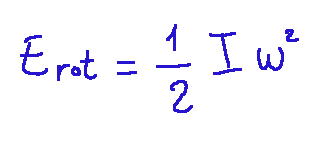
Where:
I = moment of inertia of the body
𝜔 = angular velocity
Huygens-Steiner theorem
The Huygens-Steiner theorem is used to calculate the moment of inertia of a body with respect to any axis, parallel to an axis that passes through the barycenter (center of mass) of the body.
NOTE: This theorem is also called the parallel axes theorem.
This theorem is useful because the axis does not always pass through the center of mass. Furthermore, it can avoid very complicated calculations in certain cases.
Finally, this theorem is useful in dynamics and statics when studying rotational motions of rigid bodies or equilibria of structures and beams.
Below I will show the mathematical formula without going into details:
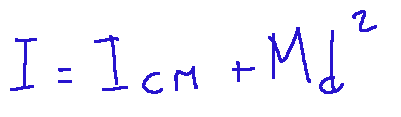
Angular momentum
Angular momentum (L) is the rotational equivalent of momentum. It is a vector quantity that describes the rotational momentum of a rotating object. Mathematically, angular momentum can be expressed as the product of the moment of inertia of an object with respect to the axis of rotation and the angular velocity. Angular momentum can be applied not only to circular motions, but also to non-circular motions under certain conditions.
Angular momentum is a fundamental quantity in the physics of rotational motion, and is the "rotational equivalent" of linear momentum
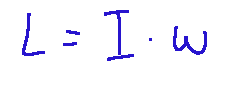
Where:
L = scalar angular momentum,
I = moment of inertia of the body,
ω = angular velocity.
Composition of motions
Rototranslation motion

image created with artificial intelligence, the software used is Microsoft Copilot
What rototranslation motion is is something that we can also guess from its name. In fact, it is the composition between a rotation and a translation. This combination is also defined as isometry, that is, a geometric transformation that leaves the distances unchanged.
We can also say that rototranslation is a rigid movement in which a geometric figure first rotates and then translates.
A classic example of this motion can be a wheel that rolls without slipping. In fact, it would have a translational motion because the center moves forward, but also a rotation mode around its own axis.
pure rolling motion
We can take inspiration from the aforementioned case of the wheel and say the following.
The simplest case of rototranslation of a rigid body is the pure rolling motion. If we take the case, for example, of a wheel that has homogeneous density we will have that the center of mass is located in its geometric center. If the wheel rolls without slipping the composition of the motion will be a translation of its center of mass and the rotation of the other points around it.
kinetic energy in rolling
The kinetic energy in rolling is the sum of two energies, that of the translational motion and that of the rotational motion. Below I show the formula of the kinetic energy in rolling, which remotely resembles the energy equation.
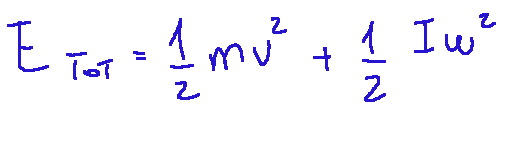
The dynamics of rolling
The dynamics of rolling is used to describe how and why a body rolls. We can say that the dynamics of rolling describes the connection between forces, translational motion and rotational motion.
We can describe the dynamics of rolling in a technical way and say the following.
In ideal conditions, if a force were applied to a wheel at rest on a horizontal plane, for example at its center of mass, it would start moving horizontally without rotating. For rolling to occur, there must therefore be a friction force between the wheel and the plane.
Since at every instant the point in contact with the ground is stationary due to this friction, we will have that this force has the form of static friction.
Conclusions
The study of rotational motion is fundamental in many industrial fields, because many objects in the real world rotate. The study of rotational motion is very important in mechanical engineering, astronautics and in the automotive industry.
Question
Rotational motions have been studied by many scientists throughout history, but did you know that the equations of rotational dynamics were mathematically described with precision by Leonhard Euler in the 18th century?

ITALIAN

13-04-2025 - Fisica - Movimento rotazionale e composizione dei moti [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_73-72)
Movimento rotazionale e composizione dei moti

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
il momento di inerzia
Il momento di inerzia è solitamente rappresentato con la lettera I.
Possiamo dire che il momento di inerzia di un corpo dotato di massa M, approssimata da un punto materiale, risulta essere il prodotto della massa del corpo per la distanza al quadrato rispetto ad un asse attorno al quale il corpo ruota.
lo possiamo definire matematicamente come segue.

Possiamo anche dire che esso rappresenta quanto posizione fa un corpo alla variazione della sua velocità angolare di rotazione attorno all’asse. L’unità di misura del momento di inerzia nel sistema internazionale è il kg m^2
Quando siamo di fronte a dei corpi rigidi dobbiamo sapere che ci sono delle formule per calcolare il momento di inerzia.
Queste formule sono presenti in alcune tabelle e descrivono i momenti di inerzia delle principali forme di corpi rigidi. Queste forme possono essere appunto il guscio cilindrico, il cilindro pieno, il cilindro cavo un’asta, un guscio sferico, una sfera oppure un parallelepipedo.
L’energia cinetica rotazionale
Ora passiamo ad introdurre il concetto di energia cinetica rotazionale. L’energia cinetica rotazionale é l’energia associata al moto di rotazione di un corpo attorno ad un asse. Possiamo anche dire che questa energia è l’equivalente rotazionale della classica energia cinetica che usiamo per il moto rettilineo, solo che in questo caso riguarda quanta energia ha un corpo che sta ruotando. La formula dell’energia cinetica rotazionale è scritta qui di seguito.
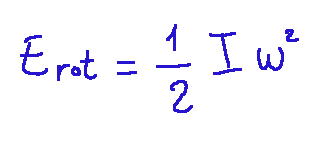
Dove:
I = momento di inerzia del corpo
𝜔 = velocità angolare
Teorema di Huygens-Steiner
Il teorema di Huygens-Steiner serve per calcolare il momento di inerzia di un corpo rispetto a un asse qualsiasi, parallelo a un asse che passa per il baricentro (centro di massa) del corpo.
NOTA: Questo teorema è chiamato anche come teorema degli assi paralleli.
Questo teorema è utile perché non sempre l’asse passa per il centro di massa. Inoltre può evitare in certi casi calcoli molto complicati.
Infine questo teorema è utile nella dinamica e nella statica quando si studiano moti rotatori di corpi rigidi o equilibri di strutture e travi.
Qui di seguito ne mostrerò la formula matematica senza entrare nei dettagli:
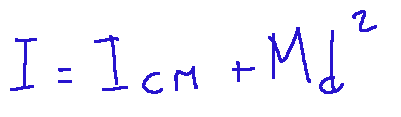
Momento angolare
Il momento angolare (L) è l'equivalente rotazionale della quantità di moto. È una quantità vettoriale che descrive il momento rotatorio di un oggetto in rotazione. Matematicamente, il momento angolare può essere espresso come il prodotto del momento d'inerzia di un oggetto rispetto all'asse di rotazione e della velocità angolare. Il momento angolare può essere applicato non solo ai moti circolari, ma anche a moti non circolari in determinate condizioni.
Il momento angolare è una grandezza fondamentale nella fisica del moto rotatorio, ed è il "corrispondente rotazionale" della quantità di moto lineare
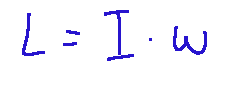
Dove:
L = momento angolare scalare,
I = momento di inerzia del corpo,
ω = velocità angolare.
La composizione dei moti
Il moto di rototraslazione

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Che cosa sia il moto di rototraslazione è qualcosa che possiamo anche intuire dal suo nome. Infatti, esso è la composizione tra una rotazione e una traslazione. Questa combinazione viene anche definita come isometria, cioè una trasformazione geometrica che lascia inalterate le distanze.
Possiamo anche dire che la rototraslazione è un movimento rigido in cui una figura geometrica, prima ruota e poi trasla.
Un esempio classico di questo moto può essere proprio una ruota che rotola senza slittare. Infatti essa avrebbe un moto di traslazione perché il centro si sposta in avanti, ma anche un modo di rotazione attorno al suo stesso asse.
moto di puro rotolamento
Possiamo prendere spunto dall'appena citato caso della ruota e dire quanto segue.
Il caso più semplice di rototraslazione di un corpo rigido è il moto di puro rotolamento. Se prendiamo il caso, per esempio, di una ruota che ha densità omogenea avremo che il centro di massa è situato nel suo centro geometrico. Se la ruota rotola senza strisciamento la composizione del moto sarà una traslazione del suo centro di massa e la rotazione degli altri punti intorno ad esso.
energia cinetica nel rotolamento
L’energia cinetica nel rotolamento è la somma di due energie quella del moto di traslazione e quella del moto di rotazione. Qui di seguito mostro la formula dell’energia cinetica nel rotolamento, che lontanamente ricorda l’equazione dell’energia.
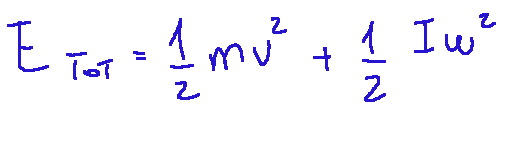
La dinamica del rotolamento
La dinamica del rotolamento viene usata per descrivere come e perché un corpo rotola. Possiamo dire che la dinamica della rotolamento descrive il legame tra le forze, il moto traslato e il moto rotatorio.
Possiamo descrivere la dinamica del rotolamento in maniera tecnica e dire quanto segue.
In condizioni ideali, se ad una ruota ferma sul piano orizzontale venisse applicata una forza, ad esempio nel suo centro di massa, si metterebbe in movimento orizzontale senza rotazione. Per fare in modo che il rotolamento avvenga è necessario quindi che tra la ruota e il piano ci sia una forza d’attrito.
Essendo in ogni istante il punto a contatto con il terreno fermo per effetto di tale attrito avremo che tale forza ha la forma di attrito statico.
Conclusioni
Lo studio del movimento rotazionale è fondamentale in tantissimi industriali, perché tantissimi oggetti nel mondo reale ruotano. Lo studio del movimento rotazionale è importantissimo in ingegneria meccanica, astronautica e nell'industria automobilistica.
Domanda
I moti rotatori sono stati studiati da diversi scienziati nel corso della storia, ma lo sapevate che le equazioni della dinamica rotazionale furono matematicamente descritti con precisione da Leonhard Euler nel XVIII sec.?
THE END
